（本题12分）如图，ABCD是一张矩形纸片，AD=BC=1,AB=CD=5．在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK．
（1）若∠1=70°，求∠MKN的度数．
（2）△MNK的面积能否小于
？若能，求出此时∠1的度数；若不能，试说明理由．
（3）如何折叠能够使△MNK的面积最大？请你利用备用图探究可能出现的情况，求出最大值．
（凉山州）如图，已知抛物线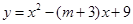
的顶点C在x轴正半轴上，一次函数
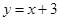与抛物线交于A、B两点，与x、y轴交于D、E两点．
（1）求m的值．
（2）求A、B两点的坐标．
（3）点P（a，b）（
）是抛物线上一点，当△PAB的面积是△ABC面积的2倍时，求a，b的值．
（资阳）学校需要购买一批篮球和足球，已知一个篮球比一个足球的进价高30元，买两个篮球和三个足球一共需要510元．
（1）求篮球和足球的单价；
（2）根据实际需要，学校决定购买篮球和足球共100个，其中篮球购买的数量不少于足球数量的
，学校可用于购买这批篮球和足球的资金最多为10500元．请问有几种购买方案？
（3）若购买篮球x个，学校购买这批篮球和足球的总费用为y（元），在（2）的条件下，求哪种方案能使y最小，并求出y的最小值．
（资阳）如图，直线
与x轴、y轴分别相交于A、B两点，与双曲线
（
）相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为（﹣2，0）．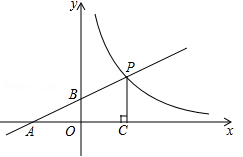
（1）求双曲线的解析式；
（2）若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与△AOB相似时，求点Q的坐标．
（资阳）已知直线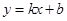
（
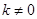）过点F（0，1），与抛物线
相交于B、C两点．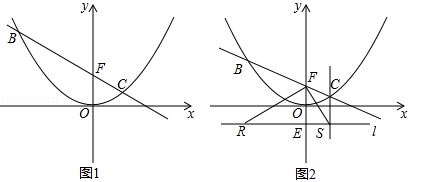
（1）如图1，当点C的横坐标为1时，求直线BC的解析式；
（2）在（1）的条件下，点M是直线BC上一动点，过点M作y轴的平行线，与抛物线交于点D，是否存在这样的点M，使得以M、D、O、F为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由；
（3）如图2，设B（m，n）（m＜0），过点E（0，﹣1）的直线l∥x轴，BR⊥l于R，CS⊥l于S，连接FR、FS．试判断△RFS的形状，并说明理由．
（宜宾）如图，抛物线
与x轴分别相交于点A（﹣2，0），B（4，0），与y轴交于点C，顶点为点P．
（1）求抛物线的解析式；
（2）动点M、N从点O同时出发，都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动，过点M作x轴的垂线交BC于点F，交抛物线于点H．
①当四边形OMHN为矩形时，求点H的坐标；
②是否存在这样的点F，使△PFB为直角三角形？若存在，求出点F的坐标；若不存在，请说明理由．