如图所示,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.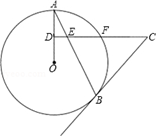
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=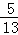 ,求⊙O的半径
,求⊙O的半径
用反证法证明:在一个三角形中,如果两条边不相等,那么这两条边所对的角也不相等.
如图,在四边形ABCD中,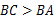 ,
,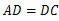 ,BD平分∠ABC.
,BD平分∠ABC.
求证:∠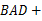 ∠
∠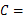 180°.
180°.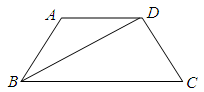
如图,在△ABC中,∠B=90°,M是AC上任意一点(M与A不重合),MD⊥BC,MD交∠BAC的平分线于点D,求证: .
.
如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)试写出点A,B之间的距离d(厘米)与时间t(秒)之间的函数表达式;
(2)问点A出发后多少秒两圆相切?
如图,己知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到C点在圆锥的侧面上的最短距离。