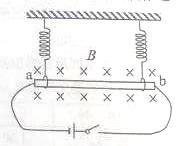
如图,一长为10cm的金属棒用两个完全相同的弹簧水平地悬挂在匀强磁场中;磁场的磁感应强度大小为0.1T,方向垂直于纸面向里;弹簧上端固定,下端与金属棒绝缘,金属棒通过开关与一电动势为12V的电池相连,电路总电阻为2。已知开关断开时两弹簧的伸长量均为0.5cm;闭合开关,系统重新平衡后,两弹簧的伸长量与开关断开时相比均改变了0.3cm,重力加速度大小取。判断开关闭合后金属棒所受安培力的方向,并求出金属棒的质量。
如图回旋加速器D形盒的半径为r,匀强磁场的磁感应强度为B.一个质量了m、电荷量为q的粒子在加速器的中央从速度为零开始加速.
(1)求该回旋加速器所加交变电场的频率;
(2)求粒子离开回旋加速器时获得的动能;
(3)设两D形盒间的加速电压为U,质子每次经电场加速后能量增加,加速到上述能量所需时间(不计在电场中的加速时间).
如图所示的示波管,质量为m,带电量为q的电子由阴极发射后,经电子枪加速水平飞入偏转电场,最后打在荧光屏上,已知加速电压为U1,偏转电压为U2,两偏转极板间距为d,板长为L1,从偏转极板到荧光屏的距离为L2,
(1)求电子离开加速电场的速度v1
(2)求电子离开偏转电场时竖直方向偏移的距离y1和偏转的角度α
(3)求电子打在荧光屏上的偏距y2.
在如图的匀强电场中,有A、B两点,且A、B两点间的距离为x=0.20m,已知AB连线与电场线夹角为θ=60°,今把一电荷量q= -2×10-8C的检验电荷放入该匀强电场中,其受到的电场力的大小为F=4.0×10-4N,方向水平向右.求: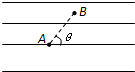
(1)电场强度E的大小和方向;
(2)若把该检验电荷从A点移到B点,电势能变化了多少;
(3)若A点为零电势点,B点电势为多少.
如图所示,电源的内电阻r=1Ω,定值电阻R=3Ω,小电动机绕组的电阻RM=0.5Ω.当开关S闭合后电路正常工作,电压表的读数U=5V,电流表的读数I=1A.求:
(1)电源的电动势E;
(2)电动机的输出功率P出.
如图所示,一闭合线圈有200匝,总电阻R=5Ω,穿过它的磁通量在0.2 s内由6×10 -3 Wb增加到1.2×10-2 Wb,求: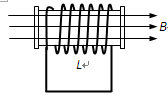
(1)线圈中磁通量的变化量
(2)线圈中磁通量的变化率
(3)线圈中产生的感应电动势E大小