滑块
沿水平面上同一条直线发生碰撞;碰撞后两者粘在一起运动;经过一段时间后,从光滑路段进入粗糙路段。两者的位置
随时间
变化的图像如图所示。求:

(ⅰ)滑块
的质量之比;
(ⅱ)整个运动过程中,两滑块克服摩擦力做的功与因碰撞而损失的机械能之比。
如右图示,两个电阻器的阻值分别为R和2R,其余电阻不计,电容器的电容 量为C,匀强磁场的磁感应强度的大小为B,方向垂直于纸面向里,金属棒ab、cd的长度均为l。当棒ab以速度v向左切割磁感 线运动,金属棒cd以速度2v向右切割磁感线运动时,电容C的电量为多大?哪一 个极板带正电?
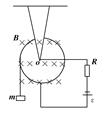
如右图示,位于水平面内的两条平行导轨相距l=0.3米;电源电动势为ε="6" 伏,内阻不计,R=5欧;金属棒ab置于导轨上,且与导轨垂直;整个装置放在图示方向的匀强磁场中,当闭合K后,金属棒运动时所受的摩擦力阻力f=0.1牛,求ab棒的最大速度vmax和vmax对应的磁 感应强度B(金属棒和导轨的电阻不计)。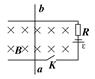
如右图示,一金属框架abcd水平放置在匀强磁场中,导体ab长为L,重为G,可以在框架上滑动,它和框架之间的摩擦系数为μ。已知磁感应强度为B,方向斜向上与框平面成θ角。导体ab的电阻为R,框 架的电阻忽略不计。现要使导体ab沿框架以速度v向右作匀速滑动,求移动ab所需 的水平力。
如图示,闭合单匝线圈在匀强磁场中以角速度ω绕中心轴OO1逆时针匀速转 动。已知:线圈的边长ab=cd=l1=0.20米,bc=da=l2=0.10米,线圈的电阻值R=0.050欧姆,角速度ω=300弧度/秒;匀强磁场的磁感应强度的大小B=0.50特,方向 与转轴OO1垂直。规定当线圈平面与B垂直,并且ab边在纸面(即过OO1轴平行于B的平面)前开始计算线圈的转角θ。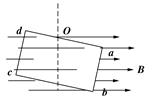
(1)当θ=ωt=30°时,线圈中感应电动势的大小、方向如何?线圈所受的电磁力矩M磁的大小、方向如何?
(2)这时,作用在线圈上的电磁力的即时功率等于多少?
铜盘的半径为r,竖直悬挂,可绕O点无摩擦地滑动,匀强磁场B垂直于圆盘, 盘边缘绕着细长线,线一端挂着质量为m的物体,电阻R与电源ε按右图示方法接到圆盘上,现欲使重物以速度v匀速提升,问所用电源电动势为多少?(设圆盘的质量不计,电阻不计,导线与圆盘连接良好)。