已知函数 (其中
(其中 )的图像与x轴的交点中,相邻两个交点之间的距离为
)的图像与x轴的交点中,相邻两个交点之间的距离为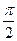 ,且图像上一个最低点为
,且图像上一个最低点为 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)当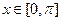 ,求
,求 的单调增区间.
的单调增区间.
设函数 在区间
在区间 上的最小值为
上的最小值为 令
令
 .
.
(Ⅰ)求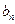 ;
;
(Ⅱ)试求所有的正整数 ,使得
,使得 为数列
为数列 中的项;
中的项;
(Ⅲ)求证: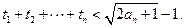
已知椭圆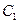 :
: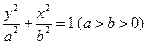 的右顶点为
的右顶点为 ,过
,过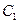 的焦点且垂直长轴的弦长为1.
的焦点且垂直长轴的弦长为1.
(Ⅰ)求椭圆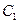 的方程;
的方程;
(Ⅱ)设点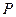 在抛物线
在抛物线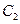 :
: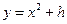
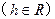 上,
上,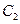 在点
在点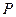 处的切线与
处的切线与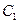 交于点
交于点 .线段
.线段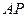 的中点与
的中点与 的中点的横坐标相等时,求
的中点的横坐标相等时,求 的最小值.
的最小值.
已知函数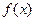 是定义在
是定义在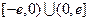 上的奇函数,当
上的奇函数,当 时
时
(Ⅰ)求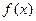 的解析式;
的解析式;
(Ⅱ)设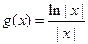 ,
,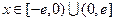 ,求证:当
,求证:当 时,
时,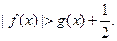
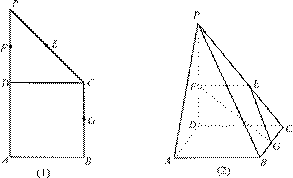
如图(1)在直角梯形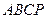 中,
中, ∥
∥
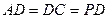 =2,
=2,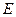 、
、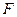 、
、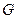 分别是
分别是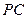 、
、 、
、 的中点,现将
的中点,现将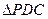 沿
沿 折起,使平面
折起,使平面 平面
平面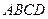 (如图2).
(如图2).
(Ⅰ)求二面角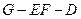 的大小;
的大小;
(Ⅱ)在线段 上确定一点
上确定一点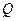 ,使
,使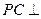 平面
平面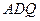 ,并给出证明过程.
,并给出证明过程.
 |