选修4-4:坐标系与参数方程
在直角坐标版权法
吕,直线
的参数方程为
(
为参数),以原点为极点,
轴的正半轴为极轴建立极坐标系,
的极坐标方程为
.
(Ⅰ)写出
的直角坐标方程;
(Ⅱ)
为直线
上一动点,当
到圆心
的距离最小时,求点
的坐标.
某工厂生产一种产品,已知该产品的月产量x吨与每吨产品的价格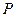 (元)之间的关系为
(元)之间的关系为 ,且生产
,且生产 吨的成本为
吨的成本为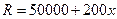 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
已知双曲线与椭圆可 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,求双曲线方程。
,求双曲线方程。
已知ΔABC的三条边分别为 求证:
求证:
某企业为考察生产同一种产品的甲、乙两条生产线的产品合格率,同时各抽取100件产品,检验后得到如下联表:
生产线与产品合格率列联表
| 合格 |
不合格 |
总计 |
|
| 甲线 |
97 |
3 |
100 |
| 乙线 |
95 |
5 |
100 |
| 总计 |
192 |
8 |
200 |
请问甲、乙两线生产的产品合格率在多大程度上有关系?(本题满分10分)
附:
 |
 |
 |
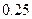 |
 |
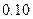 |
 |
 |
 |
 |
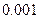 |
 |
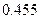 |
 |
 |
 |
 |
 |
 |
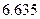 |
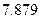 |
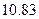 |
(本小题满分12分)
函数 )
)
(Ⅰ)已知 的展开式中
的展开式中 的系数为
的系数为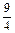 ,求常数
,求常数
(Ⅱ)已知 ,是否存在
,是否存在 的值,使
的值,使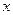 在定义域中取任意值时,
在定义域中取任意值时, 恒成立?如存在,求出
恒成立?如存在,求出 的值,如不存在,说明理由.
的值,如不存在,说明理由.