(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
⑴求证:PA∥平面BDE;
⑵求证:平面BDE⊥平面PBC.
根据统计资料,某工艺品厂的日产量最多不超过20件,每日产品废品率 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式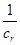 (日产品废品率
(日产品废品率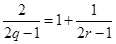
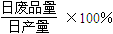 ).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润 日正品赢利额
日正品赢利额 日废品亏损额)
日废品亏损额)
(1)将该车间日利润 (千元)表示为日产量
(千元)表示为日产量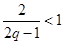 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
如图,在五面体 中,已知
中,已知 平面
平面 ,
, ,
, ,
,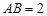 ,
,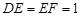 .
.
(1)求证: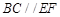 ;
;
(2)求三棱锥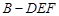 的体积.
的体积.
在△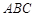 中,已知
中,已知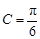 ,向量
,向量 ,
, ,且
,且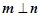 .
.
(1)求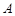 的值;
的值;
(2)若点 在边
在边 上,且
上,且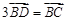 ,
,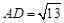 ,求△
,求△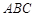 的面积.
的面积.
在数列 中,已知
中,已知 ,
, ,
, (
(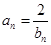 ,
, ).
).
(1)当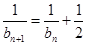 ,
, 时,分别求
时,分别求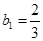 的值,判断
的值,判断 是否为定值,并给出证明;
是否为定值,并给出证明;
(2)求出所有的正整数 ,使得
,使得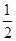 为完全平方数.
为完全平方数.
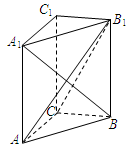
如图,在直三棱柱 中,已知
中,已知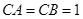 ,
, ,
,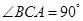 .
.
(1)求异面直线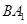 与
与 夹角的余弦值;
夹角的余弦值;
(2)求二面角 平面角的余弦值.
平面角的余弦值.