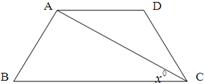
如图,在直角梯形ABCD中,AD // BC,∠B=90°,AD=24cm,BC=26cm,动点P从A点开始沿AD边向D以3cm/s的速度运动,动点Q从点C开始沿CB边向点B以1cm/s的速度运动,点P、Q分别从A、C同时出发,设运动时间为t (s).
⑴当其中一点到达端点时,另一点也随之停止运动.
①当t为何值时,以CD、PQ为两边,以梯形的底(AD或BC)的一部分(或全部)为第三边能构成一个三角形;②当t为何值时,四边形PQCD为等腰梯形.
⑵若点P从点A开始沿射线AD运动,当点Q到达点B时,点P也随之停止运动.当t为何值时,以P、Q、C、D为顶点的四边形是平行四边形.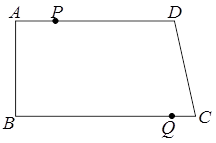
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,以△ABC的一边为边画等腰三角形,使它的第三个顶点D在△ABC的其它边上.请在图①、图②、图③中分别画出一个符合条件的等腰三角形,且三个图形中的等腰三角形各不相同,并在图下方的横线上写明所画等腰三角形的腰和腰长(要求尺规作图).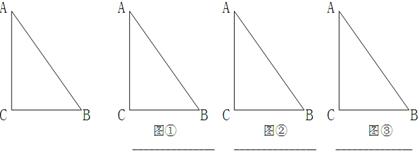
如图,在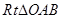 中,
中,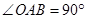 ,
,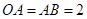 ,
,
(1) 将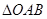 绕点
绕点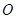 沿逆时针方向旋转
沿逆时针方向旋转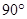 得到
得到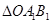 ;
;
(2) 连结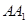 ,判断四边形
,判断四边形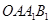 的形状,并说明理由;
的形状,并说明理由;
(3) 四边形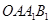 的面积是_________。
的面积是_________。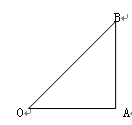
如图,E、F是平行四边形ABCD的对角线AC上的点,CE=AF,请你猜想:线段BE与线段DF有怎样的关系?并对你的猜想加以说明.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD, . 设∠ACB=
. 设∠ACB=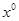 .(1)图中还有哪些角也等于
.(1)图中还有哪些角也等于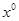 ?并说明理由.
?并说明理由.
(2)求 的值.
的值.