已知两直线 、
、 分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有 ⊥
⊥ ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线 交于点K,如图所示.
交于点K,如图所示.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得以A、B、C、P为顶点的四边形的面积等于△ABC的面积的 倍?若存在,求出点P的坐标;若不存在,请说明理由.
倍?若存在,求出点P的坐标;若不存在,请说明理由.
(3)将直线 按顺时针方向绕点C旋转α°(0<α<90°),与抛物线的另一个交点为M.求在旋转过程中△MCK为等腰三角形时的α的值.
按顺时针方向绕点C旋转α°(0<α<90°),与抛物线的另一个交点为M.求在旋转过程中△MCK为等腰三角形时的α的值.
在数轴上画出表示-1.5 ,2,-1,- 及它们的相反数的点。
及它们的相反数的点。
a与b互为相反数,c与d互为倒数,求 的值。
的值。
喜爱数学的小明一天在家里发现他妈妈刚从超市买回来的2块超能皂, 小明仔细看了超能皂外包装上的尺寸说明,每块的尺寸均是是:长(a)、宽(b)、高(c)分别是16cm,6cm,3cm.他想起老师讲过关于物体外包装用料最省的问题,就想研究这两块超能皂如何摆放,它的外包装用料才最省?
实践与操作:小明动手摆放了这2块超能皂摆放情况,发现无论怎样放置,体积都不会发生变化,但是由于摆放位置的不同,它们的外包装用料不同,经过实际操作发现这两块超能皂有3种不同的摆放方式,如图所示:
 |
①请你帮助小明指出图1,图2,图3这3种不同摆放方式的长、宽、高,并计算其外包装用料,填写在下表中(包装接头用料忽略不计)?:
| 长(cm) |
宽(cm) |
高(cm) |
表面积(cm2) |
|
| 图1 |
||||
| 图2 |
||||
| 图3 |
探究与思考:如果现在有4块这样的超能皂,如何摆放使它的外包装用料最省呢?说说你的理由
根据下面给出的数轴,解答下面的问题:
 |
⑴ 请你根据图中A、B两点的位置,分别写出它们所表示的有理数A:
B:;
⑵ 观察数轴,与点A的距离为4的点表示的数是:;
⑶ 若将数轴折叠,使得A点与-3表示的点重合,则B点与数表示的点重合;
⑷ 若数轴上M、N两点之间的距离为2010(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:N:.
有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
| 与标准质量的差值 (单位:千克) |
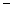 3 3 |
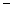 2 2 |
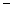 1.5 1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
2 |
8 |
⑴20筐白菜中,最重的一筐比最轻的一筐重千克
⑵与标准重量比较,20筐白菜总计超过或不足多少千克?
⑶若白菜每千克售价2元,则出售这20筐白菜可卖多少元?