(12分) 如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示。t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放。在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好。已知cd棒的质量为m、电阻为R,ab棒的质量、阻值均未知,区域Ⅱ沿斜面的长度为2l,在t=tx时刻(tx未知)ab棒恰进入区域Ⅱ,重力加速度为g。求:
(1)通过cd棒电流的方向和区域I内磁场的方向;
(2)当ab棒在区域Ⅱ内运动时,cd棒消耗的电功率;
(3)ab棒开始下滑的位置离EF的距离;
(4)ab棒开始下滑至EF的过程中回路中产生的热量。
一物体做匀变速直线运动,在t=0时,初速度v0=2m/s,加速度a =-5 m/s2,求:
(1)速度减为零时,物体距出发点多远?
(2)在 t=1s末,物体距出发点多远?
如图所示,光滑水平面上有一块木板,质量M="2.0" kg,长度L=1.0m。在木板的最右端有一个小滑块(可视为质点),质量m="1.0" kg。小滑块与木板之间的动摩擦因数μ=0.2。开始时它们都处于静止状态。某时刻起对小滑块施加一个F="5.0" N水平向左的恒力,此后小滑块将相对木板滑动。取g ="10" m/s2。求:
(1)小滑块从木板右端运动到左端所用的时间t;
(2)小滑块从木板右端运动到左端的过程中,恒力F对小滑块所做的功W;
(3)如果想缩短小滑块从木板右端运动到左端所用的时间t,只改变木板的质量M,请你通过计算,判断木板的质量M应该增大还是减小?
如图是建筑工地上常用的一种“深穴打夯机”,电动机带动两个滚轮匀速转动将夯杆从深坑提上来,当夯杆底端刚到达坑口时,两个滚轮彼此分开,将夯杆释放,夯杆在自身重力作用下,落回深坑,夯实坑底,然后两个滚轮再次压紧,夯杆被提上来,如此周而复始。已知两个滚轮边缘的线速度恒为v=4m/s,滚轮对夯杆的正压力FN=2×104kg,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆的质量m=1×103N,坑深h=6.4m,假设在打夯的过程中坑的深度变化不大,取g="10" m/s2.求: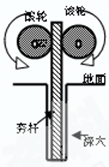
(1)每个打夯周期中,电动机对夯杆所做的功;
(2)每个打夯周期中,滚轮与夯杆间因摩擦产生的热量;
(3)打夯周期。
如图所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等。在轻绳两端C、D分别施加竖直向下的恒力F=mg。先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变。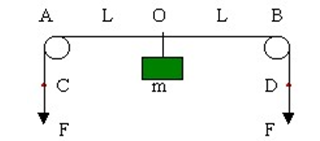
(1)当物块下落距离h为多大时,物块的加速度为零?
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为多少?
(3)求物块下落过程中的最大速度Vm和最大距离H?
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A。半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B。用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来。杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2。现给小球A一个水平向右的恒力F=55N。求: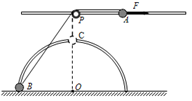
(1)把小球B从地面拉到P点正下方C点过程中,力F做的功;
(2)把小球B从地面拉到P点正下方C点过程中,重力对小球B做的功;
(3)把小球B从地面拉到P点正下方C点时,A小球速度的大小;
(4)把小球B从地面拉到P点正下方C点时,小球B速度的大小;
(5)小球B被拉到离地多高时与小球A速度大小相等。