如图所示,直角坐标系xOy位于竖直平面内,x轴与绝缘的水平面重合,在y轴右方有垂直纸面向里的匀强磁场和竖直向上的匀强电场.质量为m2=8×10-3 kg的不带电小物块静止在原点O,A点距O点l=0.045 m,质量m1=1×10-3 kg的带电小物块以初速度v0=0.5 m/s从A点水平向右运动,在O点与m2发生正碰并把部分电量转移到m2上,碰撞后m2的速度为0.1 m/s,此后不再考虑m1、m2间的库仑力。已知电场强度E=40 N/C,小物块m1与水平面的动摩擦因数为μ=0.1,取g=10 m/s2,求:
(1)碰后m1的速度;
(2)若碰后m2做匀速圆周运动且恰好通过P点,OP与x轴的夹角θ=30°,OP长为lOP=0.4 m,求磁感应强度B的大小;
(3)其他条件不变,若改变磁场磁感应强度B′的大小,使m2能与m1再次相碰,求B′的大小。
如下图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达小孔A进入半径R=0.3m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔。已知摆线长L=2m,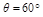 ,小球质量为m=0.5kg,D点与小孔A的水平距离s=2m,g取10m/s2。试求:
,小球质量为m=0.5kg,D点与小孔A的水平距离s=2m,g取10m/s2。试求:
(1)求摆线能承受的最大拉力为多大?
(2)若小球能进入圆轨道后恰好能做圆周运动,求粗糙水平面动摩擦因数μ。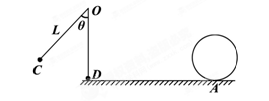
如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3秒后又恰好垂直与倾角为450的斜面相碰到。已知圆轨道半径为R=1m,小球的质量为m=1kg,g取10m/s2。求
(1)小球在斜面上的相碰点C与B点的水平距离
(2)小球经过圆弧轨道的B点时,受到轨道的作用力
NB的大小和方向?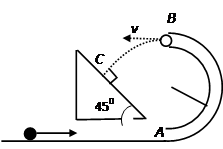
已知“天宫一号”在地球上空的圆轨道上运行时离地面的高度为h.地球半径为R,地球表面的重力加速度为g.求:
(1)地球的密度为多少
(2)“天宫一号”在该圆轨道上运行时速度v的大小;
汽车与路面的动摩擦因数为μ,公路某转弯处半径为R(设最大静摩擦力等于滑动摩擦力),问:
(1)若路面水平,汽车转弯不发生侧滑,对汽车最大速度为多少?
(2)若将公路转弯处路面设计成外侧高、内侧低,使路面与水平面倾角为α,则汽车以多大速度转弯,可以使车与路面间无摩擦力?
如图 (a)所示,质量m=1 kg的物体沿倾角θ=37°的固定粗糙斜面由静止开始向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k表示,物体加速度a与风速v的关系如图(b)所示,求:
(1)物体与斜面间的动摩擦因数μ;
(2)比例系数k.(sin37°=0.6,cos37°=0.8,g=10 m/s2)