(满分14分)几何模型:
如图1, 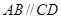 ,O是BD的中点,求证:
,O是BD的中点,求证: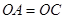 ;
;
模型应用:
(温馨提示:模型应用是指应用模型结论直接解题)
(1)如图2,在梯形ABCD中,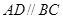 ,点E是腰DC的中点,AE平分
,点E是腰DC的中点,AE平分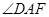 ,求证:AE⊥EF;
,求证:AE⊥EF;
(2)如图3,在⊙O中,AB是⊙O的直径,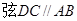 ,点E是OD的中点,点O到AC的距离为1
,点E是OD的中点,点O到AC的距离为1 ,试求阴影部分的面积.
,试求阴影部分的面积. 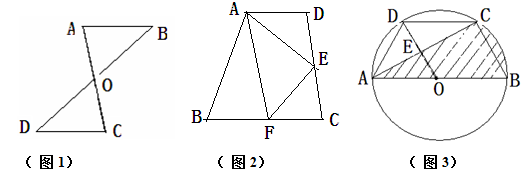
有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和﹣2;乙袋中有3个完全相同的小球,分别标有数字﹣2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为 x,再从乙袋中随机取出1个小球,记录标有的数字为 y,这样确定了点 Q的坐标( x, y)
(1)写出先 Q所有可能的坐标;
(2)求点 Q在 x轴上的概率.
如图,△ ABC中, AD⊥ BC,垂足是 D,若 BC=14, AD=12,tan∠ BAD= ,求sin C的值.

已知抛物线 y= ax 2+ bx+ c经过 A(﹣1,0), B(4,0), C(0,﹣2)三点.
(1)请直接写出抛物线的解析式.
(2)连接 BC,将直线 BC平移,使其经过点 A,且与抛物线交于点 D,求点 D的坐标.
(3)在(2)中的线段 AD上有一动点 E(不与点 A、点 D重合),过点 E作 x轴的垂线与抛物线相交于点 F,当点 E运动到什么位置时,△ AFD的面积最大?求出此时点 E的坐标和△ AFD的最大面积.

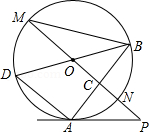
如图, PA为⊙ O的切线, A为切点,直线 PO交⊙ O于点 M、 N,过点 A作 PO的垂线 AB,垂足为 C,交⊙ O于点 B,延长 BO与⊙ O交于点 D,连接 AD、 BM.
(1)等式 OD 2= OC• OP成立吗?若成立,请加以证明;若不成立,请说明理由.
(2)若 AD=6,tan∠ M= ,求sin∠ D的值.
在我市双城同创的工作中,某社区计划对1200 m 2的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为300 m 2区域的绿化时,甲队比乙队少用3天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工 x天,再由乙队施工 y天,刚好完成绿化任务,求 y与 x的函数关系式.
(3)若甲队每天绿化费用为0.4万元,乙队每天绿化费用为0.15万元,且甲、乙两队施工的总天数不超过14天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.