（本题8分）某学校举行“社会主义核心价值观”知识比赛活动，全体学生都参加比赛，学校对参赛学生均给与表彰，并设置一、二、三等奖和纪念奖共四个奖项，赛后将获奖情况绘制成如下所示的两幅不完整的统计图，请根据图中所给的信息，解答下列问题：
（1）该校共有 名学生；
（2）在图1中，“三等奖”随对应扇形的圆心角度数是 ；
（3）将图2补充完整；
（4）从该校参加本次比赛活动的学生中随机抽查一名．求抽到获得一等奖的学生的概率．
列方程或方程组解应用题：
在平谷区桃花节来临之际，某中学团委从八年级学生中派出160人参加街道清洁工作，除八年级团员全部参加外，还派出一些非团员参加．已知派出的非团员人数是团员人数的2倍还多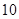
人．求参加清洁工作的团员和非团员各多少人？
已知：如图，在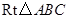
中，∠BAC=90°，AB=AC，D是
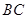边上一点，
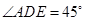，AD=DE.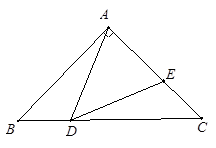
求证：BD=EC
已知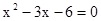
，求
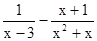的值.
如图，已知在平面直角坐标系xOy中，直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA＝AB＝2，OC＝3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．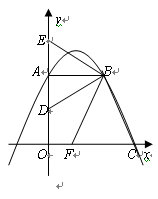
（1）求经过A、B、C三点的抛物线的解析式；
（2）当BE经过（1）中抛物线的顶点时，求CF的长；
（3）在抛物线的对称轴上取两点P、Q（点Q在点P的上方），且PQ＝1，要使四边形BCPQ的周长最小，求出P、Q两点的坐标．
如图1，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿CB方向平移得到的，连结AE，AC和BE相交于点O.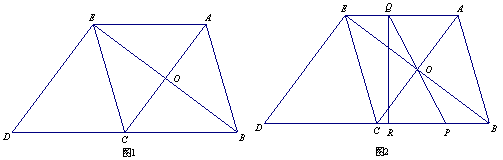
（1）判断四边形ABCE是怎样的四边形，并证明你的结论；
（2）如图2，P是线段BC上一动点（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求出四边形PQED的面积；
②当线段BP的长为何值时，以点P、Q、R为顶点的三角形与△BOC相似？