如图，抛物线y﹣x2bxc交x轴于点A，交y轴于点B，已知经-优题课

如图，抛物线y=﹣x²+bx+c交x轴于点A，交y轴于点B，已知经过点A，B的直线的表达式为y=x+3．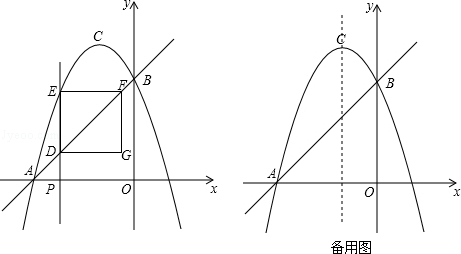

（1）求抛物线的函数表达式及其顶点C的坐标；
（2）如图①，点P（m，0）是线段AO上的一个动点，其中﹣3＜m＜0，作直线DP⊥x轴，交直线AB于D，交抛物线于E，作EF∥x轴，交直线AB于点F，四边形DEFG为矩形．设矩形DEFG的周长为L，写出L与m的函数关系式，并求m为何值时周长L最大；
（3）如图②，在抛物线的对称轴上是否存在点Q，使点A，B，Q构成的三角形是以AB为腰的等腰三角形？若存在，直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数在给定区间上的最值

求方程 $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{5}{6}$ 的正整数解．

（1）求方程 $2 x - 5 y = 4$ 的全部整数解．

（2）求方程 $7 x + 19 y = 213$ 的所有正整数解．

《中学生体质健康标准》规定学生体质健康等级标准为： $86$ 分及以上为优秀； $76$ 分~ $85$ 分为良好； $60$ 分~ $75$ 分为及格； $59$ 分以下为不及格.某校抽取八年级学生人数的 $10 %$ 进行体质测试，测试结果如图.

（1）在抽取的学生中不及格人数所占的百分比是＿＿＿＿＿；

（2）小明按以下方法计算所抽取学生测试结果的平均分是 $(90 + 82 + 65 + 40) \div 4 = 69.25$ .根据所学的统计知识判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果；

（3）若抽取的学生中不及格学生的总分恰好等于某一个良好等级学生的分数，请估算该校八年级学生中优秀等级的人数.

新安商夏对销量较大的 $A, B, C$ 三种品牌的洗衣粉进行了问卷调查，发放问卷 $270$ 份（问卷由单选和多选题组成）.对收回的 $238$ 份问卷进行了整理，部分数据如下：

最近一次购买各品牌洗衣粉用户的比例

用户对各品牌洗衣粉满意情况汇总表

根据上述信息回答下列问题：

（1） $A$ 品牌洗衣粉的主要竞争优势是什么?你是怎样看出来的?

（2）广告对用户选择品牌有影响吗?请简要说明理由.

（3）你对厂家有何建议?

如图某文具店王经理统计了2019年1月至5月 $A, B, C$ 这三种型号的钢笔平均每月的销售量，并绘制图1（不完整）.销售这三种型号钢笔平均每月获得的总利润为 $600$ 元，每种型号钢笔获得的利润分布情况如图2，已知 $A, B, C$ 这三种型号钢笔每支的利润分别是 $0.5$ 元， $0.6$ 元， $1.2$ 元，请你结合图中的信息，解答下列问题：

（1）求出 $C$ 种型号钢笔平均每月的销售量，并将图1补充完整；

（2）王经理计划6月份购进 $A, B, C$ 这三种型号的笔共 $900$ 支，请你结合1月至5月平均每月的销售情况（不考虑其它因素），设计一个方案，使获得的利润最大，并说明理由.

试卷网试题网古诗词网作文网范文网