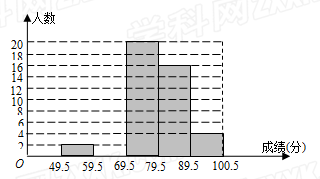
某班体育委员小华对本班近期体育测验成绩（成绩取整数，满分为100分）作了统计分析，绘制成如下频数、频率分布表和频数分布直方图．请你根据图表提供的信息，解答下列问题：
（1）频数、频率分布表中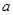
= ，
= ；
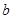（2）补全频数分布直方图；
（3）班主任准备从不低于90分的学生中选1人介绍学习经验，那么取得了93分的小华被选上的概率是多少？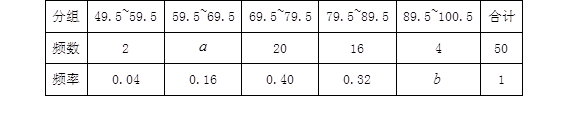
在平面直角坐标系xOy中，已知A（2，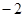
），在y轴上确定点P，使△AOP为等腰三角形，探究符合条件的点P的个数.
在下面的八幅图案中，②③④⑤⑥⑦⑧中的哪个图案可以通过平移图案①得到？
如图，已知射线DM与直线BC交于点A，AB∥DE.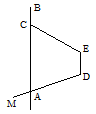
（1）若当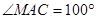
，
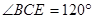时，问把EC绕点E再旋转多大角度时，可判定MD∥EC，请你设计出两种方案，并画出草图（旋转后若EC与AB相交，则交点用
表示）.
（2）若将EC绕点E逆时针旋转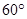
时，点C与点A恰好重合，请画出草图，并在图中找出同位角、内错角各两对（先用数字标出角，再回答）.
如图，四边形ABCD中，∠A ="∠C=" 90°，BE平分∠ABC，DF平分∠ADC，则BE与DF有何位置关系？试说明理由。
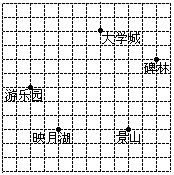
请你在下图中建立适当的直角坐标系，并写出各地点的坐标。。