如图,山脚下有一棵树AB,小华从点B沿山坡向上走50米到达点D,用 高为1.5米的测角仪CD测得树顶的仰角为10°,已知山坡的坡角为15°,求树AB的高.(精确到0.1米)
(已知sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, sin15°≈0.26, cos15°≈0.97, tan15°≈0.27.)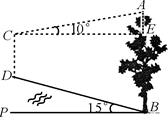
(2014中考真题)阅读下面材料:
小腾遇到这样一个问题:如图1,在 中,点
中,点 在线段
在线段 上,
上,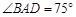 ,
, ,
,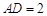 ,
,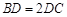 ,求
,求 的长.
的长.
小腾发现,过点 作
作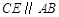 ,交
,交 的延长线于点
的延长线于点 ,通过构造
,通过构造 ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).
请回答: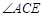 的度数为 ,
的度数为 , 的长为 .
的长为 .
参考小腾思考问题的方法,解决问题:
如图3,在四边形 中,
中, ,
, ,
, ,
, 与
与 交于点
交于点 ,
, ,
, ,求
,求 的长.
的长.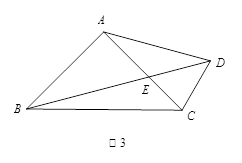
如图,在矩形ABCD中,AB=12 cm,BC=6 cm,点P沿AB边从A向B以2 cm/s的速度移动;点Q沿DA边从D向A以1 cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动时间(0≤t≤6),那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积,你有什么发现?
(3)当t为何值时,以点A,P,Q为顶点的三角形与△ABC相似?
如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,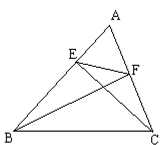
(1)求证:ΔABF ∽ΔACE
(2)求证:ΔAEF ∽ΔACB
(3)若∠A=60°,求: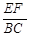
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
如图,线段BE上有一点C,以BC、CE为边分别在BE的同侧作等边三角形ABC、DCE,连结AE、BD,分别交CD、CA于Q、P.
(1)找出图中的一组相等的线段(等边三角形的边长相等除外),并说明你的理由.
(2)取AE的中点M、BD的中点N,连结MN,试判断△CMN的形状.