温度通常有两种表示方法:华氏度(单位: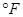 )与摄氏度(单位:
)与摄氏度(单位: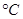 ),已知华氏度数
),已知华氏度数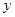 与摄氏度数
与摄氏度数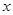 之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:
之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系: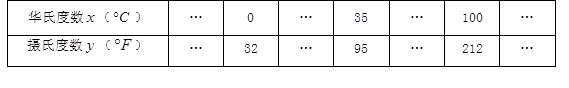
(1)选用表格中给出的数据,求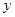 关于
关于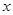 的函数解析式(不需要写出该函数的定义域);
的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是-5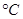 ,求与之对应的华氏度数;
,求与之对应的华氏度数;
解方程:
【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
福鼎有着丰富的旅游资源,如闻名遐迩的海上仙都太姥山、“碧海金沙”的牛郞岗海滨景区、江南古民居之杰作——翠郊古民居、风景宜人的小白鹭海滨度假村、“海上公园”台山岛、“最美海岛”之——嵛山岛等,这些都是人们节假日休闲的好去处。旅行社为了吸引游客去海上仙都太姥山和“最美海岛”之——嵛山岛旅游,推出如下的收费标准:
①如果人数不超过25人,人均旅游费用为350元.
②如果人数超过25人,每增加1人,人均旅游费用降低10元,但人均旅游费用不得低于290元.
某单位组织员工去福鼎太姥山和嵛山岛旅游,共支付费用8960元,请问该单位这次共有多少名员工参加旅游?
甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积 大于10,那么甲获胜;如果积不大于10,那么乙获胜.请你解决下列问题:
(1)利用树状图(或列表)的方法表示游戏所有可能出现的结果;
(2)求甲、乙两人获胜的概率.