已知函数 ,则下列关于函数
,则下列关于函数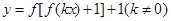 的零点个数的判断正确的是
的零点个数的判断正确的是
A.当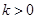 时,有3个零点;当 时,有3个零点;当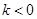 时,有4个零点 时,有4个零点 |
B.当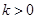 时,有4个零点;当 时,有4个零点;当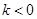 时,有3个零点 时,有3个零点 |
C.无论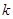 为何值,均有3个零点 为何值,均有3个零点 |
D.无论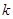 为何值,均有4个零点[来 为何值,均有4个零点[来 |
由无理数引发的数学危机一直延续到19世纪,直到1872年,德国数学家戴德金提出了“戴德金分割”,才结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集 划分为两个非空的子集
划分为两个非空的子集 与
与 ,且满足
,且满足 ,
, ,
, 中的每一个元素都小于
中的每一个元素都小于 中的每一个元素,则称
中的每一个元素,则称 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割 ,下列选项中不可能成立的是
,下列选项中不可能成立的是
A. 没有最大元素, 没有最大元素, 有一个最小元素 有一个最小元素 |
B. 没有最大元素, 没有最大元素, 也没有最小元素 也没有最小元素 |
C. 有一个最大元素, 有一个最大元素, 有一个最小元素 有一个最小元素 |
D. 有一个最大元素, 有一个最大元素, 没有最小元素 没有最小元素 |
如图,面积为 的平行四边形
的平行四边形 ,对角线
,对角线 ,
, 与
与 交于点
交于点 ,某指数函数
,某指数函数 ,经过点
,经过点 ,则
,则

A.  |
B. |
C. |
D. |
已知定义在 上的函数
上的函数 为偶函数,
为偶函数, ,则
,则 的大小关系为
的大小关系为
A. |
B. |
C. |
D. |
定义两种运算: 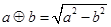 ,
,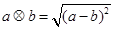 ,则函数
,则函数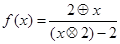 的解析式为
的解析式为
A.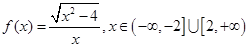 |
B.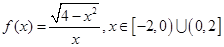 |
C.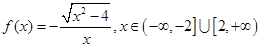 |
D.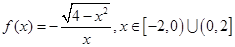 |
我们处在一个有声世界里,不同场合,人们对声音的音量会有不同要求.音量大小的单位是分贝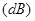 ,对于一个强度为
,对于一个强度为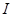 的声波,其音量的大小
的声波,其音量的大小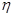 可由如下公式计算:
可由如下公式计算: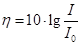 (其中
(其中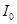 是人耳能听到的声音的最低声波强度),设
是人耳能听到的声音的最低声波强度),设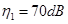 的声音强度为
的声音强度为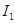 ,
,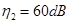 的声音强度为
的声音强度为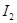 ,则
,则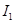 是
是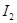 的
的
A.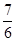 倍 倍 |
B.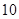 倍 倍 |
C.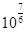 倍 倍 |
D.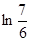 倍 倍 |