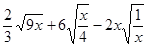如图所示，在平面直角坐标系中，点A，B，C的坐标分别为A（－2，5），B（－3，－1），C（1，－1），在第一象限内找一点D，使四边形ABCD是平行四边形，求点D的坐标．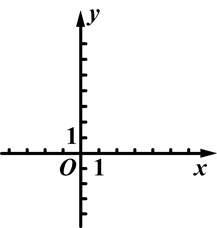
（本题满分为8分）某商店如果将进价为8元的商品按每件10元售出，每天可销售200件，现采用提高售价，减小进货量的办法增加利润，已知这种商品每涨价0.5元，其销售量就减少10件，问应将售价定为多少元时，才能使每天所获利润为640元？
（本题满分为8分）黄梅赛洛天燃气公司准备为三个村庄A、B、C铺设一条燃气管道，已知A、B、C正好位于一个等边三角形的三个顶点，现有三种铺设方案，请通过计算说明哪种方案最省.
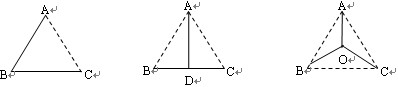
（本题满分为8分）已知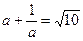
，求（1）
；（2）
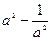的值.
（本题满分为6分）已知关于x的方程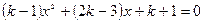
有两个不相等的实数根x1,x2，求k的取值范围.
解答过程：根据题意，得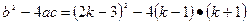
=
=
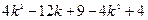
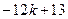＞0
∴k＜
所以当k＜时，方程有两个不相等的实数根.
当你读了上面的解答过程后，请判断是否有错误？如果有，请指出错误之处，并写出正确的答案.
（本题满分为6分）化简：