已知椭圆C: 的离心率为
的离心率为 ,
, 是椭圆的两个焦点,
是椭圆的两个焦点, 是椭圆上任意一点,且
是椭圆上任意一点,且 的周长是
的周长是 .
.
(1)求椭圆C的方程;
(2)设圆T: ,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在
,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在 轴上移动且
轴上移动且 时,求EF的斜率的取值范围.
时,求EF的斜率的取值范围.
已知向量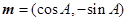 ,
,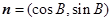 ,
,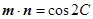 ,其中
,其中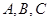 为
为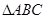 的内角.
的内角.
(Ⅰ)求角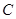 的大小;
的大小;
(Ⅱ)若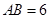 ,且
,且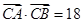 ,求
,求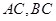 的长.
的长.
设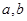 为实数,我们称
为实数,我们称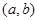 为有序实数对.类似地,设
为有序实数对.类似地,设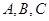 为集合,我们称
为集合,我们称 为有序三元组.如果集合
为有序三元组.如果集合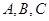 满足
满足 ,且
,且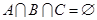 ,则我们称有序三元组
,则我们称有序三元组 为最小相交(
为最小相交(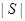 表示集合
表示集合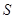 中的元素的个数).
中的元素的个数).
(Ⅰ)请写出一个最小相交的有序三元组,并说明理由;
(Ⅱ)由集合 的子集构成的所有有序三元组中,令
的子集构成的所有有序三元组中,令 为最小相交的有序三元组的个数,求
为最小相交的有序三元组的个数,求 的值.
的值.
在平面直角坐标系 中,已知曲线
中,已知曲线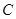 上任意一点到点
上任意一点到点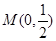 的距离与到直线
的距离与到直线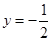 的距离相等.
的距离相等.
(Ⅰ)求曲线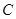 的方程;
的方程;
(Ⅱ)设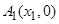 ,
, 是
是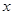 轴上的两点
轴上的两点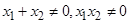 ,过点
,过点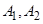 分别作
分别作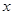 轴的垂线,与曲线
轴的垂线,与曲线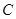 分别交于点
分别交于点 ,直线
,直线 与x轴交于点
与x轴交于点 ,这样就称
,这样就称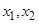 确定了
确定了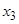 .同样,可由
.同样,可由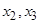 确定了
确定了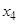 .现已知
.现已知 ,求
,求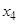 的值.
的值.
设实数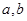 满足
满足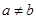 ,求证:
,求证: .
.
已知曲线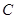 的极坐标方程为
的极坐标方程为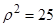 ,曲线
,曲线 的极坐标方程为
的极坐标方程为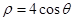 .试求曲线
.试求曲线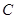 和
和 的直角坐标方程,并判断两曲线的位置关系.
的直角坐标方程,并判断两曲线的位置关系.