(本小题满分1 4分)已知椭圆 的一个焦点与抛物线
的一个焦点与抛物线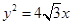 的焦点
的焦点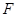 重合,且椭圆短轴的两个端点与
重合,且椭圆短轴的两个端点与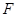 构成正三角形.
构成正三角形.
(1)求椭圆的方程:
(2)若过点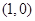 的直线
的直线 与椭圆交于不同两点
与椭圆交于不同两点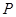 ,
,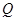 ,试问在
,试问在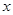 轴上是否存在定点
轴上是否存在定点 ,使
,使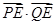
恒为定值?若存在,求出 的坐标及定值;若不存在,请说明理由.
的坐标及定值;若不存在,请说明理由.
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ)求X的分布列;
(Ⅱ)求X的数学期望E(X).
已知定义域为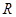 的函数
的函数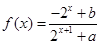 是奇函数。
是奇函数。
(Ⅰ)求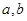 的值;
的值;
(Ⅱ)若对任意的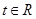 ,不等式
,不等式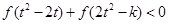 恒成立,求
恒成立,求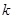 的取值范围;
的取值范围;
已知数列 中,
中,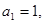 且点
且点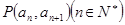 在直线
在直线 上。
上。
(1)求数列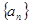 的通项公式;
的通项公式; (2)
(2) 求函数
求函数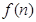 的最小值;
的最小值;
(3)设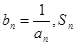 表示数列
表示数列 的前
的前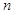 项和。试问:是否存在关于
项和。试问:是否存在关于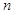 的整式
的整式 ,使得
,使得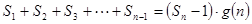 对于一切不小于2的自然数
对于一切不小于2的自然数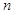 恒成立?若存在,写出
恒成立?若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
如图,在平面直角坐标系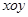 中,点
中,点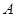 为椭圆
为椭圆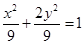 的右顶点, 点
的右顶点, 点 ,点
,点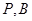 在椭圆上,
在椭圆上,  .
.
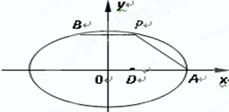
(1)求直线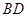 的方程;
的方程;
(2)求直线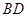 被过
被过 三点的圆
三点的圆 截得的弦长;
截得的弦长;
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交 元(
元( 为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与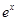 (e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值。