已知中心在原点,焦点在坐标轴上的椭圆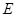 的方程为
的方程为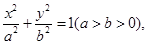 它的离心率为
它的离心率为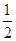 ,一个焦点是
,一个焦点是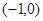 ,过直线
,过直线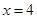 上一点引椭圆
上一点引椭圆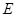 的两条切线,切点分别是A、B.
的两条切线,切点分别是A、B.
(Ⅰ)求椭圆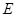 的方程;
的方程;
(Ⅱ)若在椭圆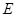
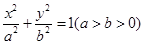 上的点
上的点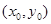 处的切线方程是
处的切线方程是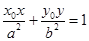 .求证:直线AB恒过定点,并求出定点的坐标;
.求证:直线AB恒过定点,并求出定点的坐标;
(Ⅲ)记点C为(Ⅱ)中直线AB恒过的定点,问否存在实数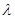 ,使得
,使得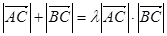 成立,若成立求出
成立,若成立求出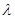 的值,若不存在,请说明理由
的值,若不存在,请说明理由
(本小题满分12分).如图是某直三棱柱被削去上底后所得几何体的直观图、左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示。
(Ⅰ)求该几何体的体积;
(Ⅱ)求证:EM∥平面ABC;
(本小题满分12分)
某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X |
1 |
2 |
3 |
4 |
5 |
| 频率 |
a |
0.2 |
0.4 |
b |
c |
(I)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(Ⅱ)在(I)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
(本小题满分12分)
在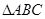 中,
中,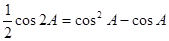 .
.
(I)求角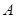 的大小;
的大小;
(II)若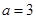 ,
,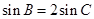 ,求
,求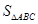 .
.
(设函数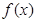 在
在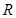 上满足
上满足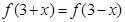 ,
,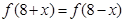 ,且
,且
在闭区间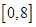 上只有
上只有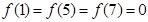 .
.
(1)求证函数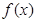 是周期函数;
是周期函数;
(2)求函数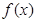 在闭区间
在闭区间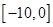 上的所有零点;
上的所有零点;
(3)求函数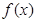 在闭区间
在闭区间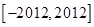 上的零点个数及所有零点的和.
上的零点个数及所有零点的和.
10分)某太阳能热水器厂2007年的年生产量为670台,该年比上一年的年产量的
增长率为34%. 从2008年开始,以后的四年中,年生产量的增长率逐年递增2%(如,2008
年的年生产量的增长率为36%).
(1)求2008年该厂太阳能热水器的年生产量(结果精确到0.1台);
(2)求2011年该厂太阳能热水器的年生产量(结果精确到0.1台);
(3)如果2011年的太阳能热水器的实际安装量为1420台,假设以后若干年内太阳能热水
器的年生产量的增长率保持在42%,到2015年,要使年安装量不少于年生产量的95%,这四
年中太阳能热水器的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?
(参考数据: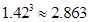 ,
,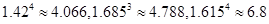 ,1.5634="5.968" ).
,1.5634="5.968" ).