如图,在□ABCD中,E、F是对角线BD上的两点,且BE=DF,连接AE、CF.请你猜想:AE与CF有怎样的数量关系,并对你的猜想加以证明.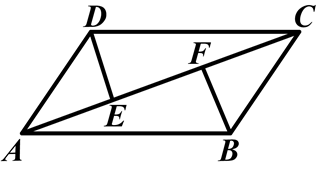
如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(即NC=4.5米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.
直线l过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP= ,求二次函数关系式.
,求二次函数关系式.
正方形ABCD中,点E是CD的中点,点F在BC上,且CF:BC=1:4,你能说明AE:EF=AD:EC吗?
如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)指定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段;
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
定义:a是不为1的有理数,我们把 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是 =−1,-1的差倒数是
=−1,-1的差倒数是 =
= .已知a1=
.已知a1= ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
(1)计算:a2=__________,a3=__________.
(2)这列数有什么规律?根据你发现的规律计算a2015的值.