如图所示,已知DF∥AC,∠1=∠2,则DE与AB平行吗?为什么?
计算: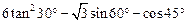
如图,已知抛物线与 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点 .
.
(1)求抛物线的解析式及其顶点 的坐标;
的坐标;
(2)设直线 交
交 轴于点
轴于点 .在线段
.在线段 的垂直平分线上是否存在点
的垂直平分线上是否存在点 ,使得点
,使得点 到直线
到直线 的距离等于点
的距离等于点 到原点
到原点 的距离?如果存在,求出点
的距离?如果存在,求出点 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;
(3)过点 作
作 轴的垂线,交直线
轴的垂线,交直线 于点
于点 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
已知一个直角三角形纸片 ,其中
,其中 .如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边
.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边 交于点
交于点 ,与边
,与边 交于点
交于点 .
.
(1)若折叠后使点 与点
与点 重合,求点
重合,求点 的坐标;
的坐标;
(2)若折叠后点 落在边
落在边 上的点为
上的点为 ,设
,设 ,
, ,试写出
,试写出 关于
关于 的函数解析式,并确定
的函数解析式,并确定 的取值范围;
的取值范围;
(3)若折叠后点 落在边
落在边 上的点为
上的点为 ,且使
,且使 ,求此时点
,求此时点 的坐标.
的坐标.
某公司有 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
 型利润 型利润 |
 型利润 型利润 |
|
| 甲店 |
200 |
170 |
| 乙店 |
160 |
150 |
(1)设分配给甲店 型产品
型产品 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为 (元),求
(元),求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店 型产品让利销售,每件让利
型产品让利销售,每件让利 元,但让利后
元,但让利后 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店 型产品的每件利润.甲店的
型产品的每件利润.甲店的 型产品以及乙店的
型产品以及乙店的 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线;
(3)若过A,D,C三点的圆的半径为 ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.