如图,已知在Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由:
(2)连接CG,求证:四边形CBEG是正方形.(提示:旋转前后,图形中对应的角和对应的边分别相等)
问题:如图(12),在菱形 和菱形
和菱形 中,点
中,点 在同一条直线上,
在同一条直线上,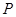 是线段
是线段 的中点,连结
的中点,连结 .探究
.探究 与
与 的位置关系及
的位置关系及 的值.小聪同学的思路是:延长
的值.小聪同学的思路是:延长 交
交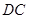 于点
于点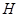 ,构造全等三角形,经过推理使问题得到解决.
,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:若图(12)中
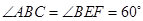 ,写出线段
,写出线段 与
与 的位置关系及
的位置关系及 的值,并说明理由;
的值,并说明理由;将图(12)中的菱形
 绕点
绕点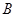 顺时针旋转,使菱形
顺时针旋转,使菱形 的对角线
的对角线 恰好与菱形
恰好与菱形 的边
的边 在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.若图(12)中
 ,将菱形
,将菱形 绕点
绕点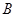 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出 的值(用含
的值(用含 的式子表示).
的式子表示).
解:(1)线段 与
与 的位置关系是;
的位置关系是; .
.
如图(11),梯形ABCD,AB∥CD ,AB=2cm,且∠OAB=30°,∠OBA=45°,梯形ABCD内部的⊙O分别切四边于E,F,M,N,
求出⊙O的半径OM的长度
求出梯形ABCD的周长.
如图(10),梯形 中,
中, ,点
,点 是边
是边 的中点, 连结
的中点, 连结 交
交 于点
于点 ,
, 的延长线交
的延长线交 的延长线于点
的延长线于点 .
.
求证:

若
 ,
, ,求线段
,求线段 的长
的长
已知关于x的一元二次方程x2 = 2(1-m)x-m2 的两实数根为x1,x2.求m的取值范围
设y = x1 + x2,当y取得最小值时,求相应m的值,并求出最小值.
为了解学生的课余生活情况,某中学在全校范围内随机抽取部分学生进行问卷调查. 问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图和条形统计图(如图(9)所示).请根据所给的扇形图和条形图,填写出扇形图中缺失的数据,并把条形图补充完整;
在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率;