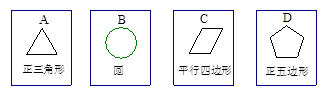小刚上午7:30从家里出发步行上学,途经少年宫时走了1200步,用时10分钟,到达学校的时间是7:55.为了估测路程等有关数据,小刚特意在学校的田径跑道上按上学的步行速度走完100米,用了150步.
(1)小刚步行的平均速度是多少米/分?小刚家和少年宫之间、少年宫和学校之间的距离分别是多少米?
(2)下午4:00,小刚从学校出发,以45米/分的速度行走,按上学时原路回家,在离少年宫300米处(还未到少年宫)与同伴玩了半小时后,赶紧以110米/分的速度回家,中途没有再停留.问:
①小刚到家的时间是下午几时?
②若小刚回家过程中,离家的路程s(米)与时间t(分)之间的函数关系如图,请写出点B的坐标.
某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
| 员工 |
管理人员 |
普通工作人员 |
|||||
| 人员结构 |
总经理 |
部门经理 |
科研人员 |
销售人员 |
高级技工 |
中级技工 |
勤杂工 |
| 员工数(名) |
1 |
3 |
2 |
3 |
 |
24 |
1 |
| 每人月工资(元) |
21000 |
8400 |
2025 |
2200 |
1800 |
1600 |
950 |
请你根据上述内容,解答下列问题:
该公司“高级技工”有名;
所有员工月工资的平均数为2500元,中位数为元,众数为元;
小张到这家公司应聘普通工作人员.
请你回答右图中小张的问题,并指出用⑵中的哪个数据向小张介绍员工的月工资实际水平更合理些;去掉四个管理人员的工资后,请你计
算出其他员工的月平均工资y(结果保留整数),并判断y能否反映该公司员工的月工资实际水平.
如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .
用含α的式子表示h(不必指出α的取值范围);
当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?(
 取1.73)
取1.73)
在下图中,每个正方形由边长为1 的小正方形组成: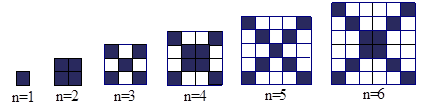
观察图形,请填写下列表格:
| 正方形边长 |
1 |
3 |
5 |
7 |
… |
 (奇数) (奇数) |
| 黑色小正方形个数 |
… |
| 正方形边长 |
2 |
4 |
6 |
8 |
… |
 (偶数) (偶数) |
| 黑色小正方形个数 |
… |
在边长为
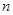 (n≥1)的正方形中,设黑色小正方形的个数为
(n≥1)的正方形中,设黑色小正方形的个数为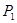 ,白色小正方形的个数为
,白色小正方形的个数为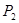 ,问是否存在偶数
,问是否存在偶数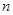 ,使
,使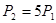 ?若存在,请写出
?若存在,请写出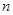 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
将图⑴中的矩形ABCD沿对角线 剪开,再把△ABC沿着AD方向平移,得到图⑵中的△A′BC′,除△ADC与△C′BA′全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明.
剪开,再把△ABC沿着AD方向平移,得到图⑵中的△A′BC′,除△ADC与△C′BA′全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明.
有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A,B,C,D表示);
求摸出两张牌面图形都是中心对称图形的纸牌的概率.