时钟在正常运行时,分针每分钟转动6°,时针每分钟转动0.5°.在运行过程中,时针与分针的夹角会随着时间的变化而变化.设时针与分针的夹角为y(度),运行时间为t(分),若时间从12:00开始到12:30止,则y与t之间的函数图象是( )
A. |
B. |
C.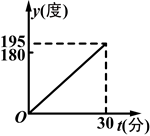 |
D. |
抛物线 可以由抛物线
可以由抛物线 平移得到,则下列平移过程正确的是
平移得到,则下列平移过程正确的是
| A.先向左平移2个单位,再向上平移3个单位 |
| B.先向左平移2个单位,再向下平移3个位 |
| C.先向右平移2个单位,再向下平移3个单位 |
| D.先向右平移2个单位,再向上平移3个单位 |
下列四个图形中,既是轴对称图形,又是中心对称图形是
| A.⑴、⑵ | B.⑴、⑶ | C.⑴、⑷ | D.⑵、⑶ |
下列运算正确的是
A.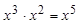 |
B.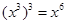 |
C.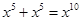 |
D.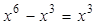 |
﹣2的绝对值等于
| A.2 | B.﹣2 | C. |
D.±2 |
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如
(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1)…根据这个规律探索可得,第100个点的坐标为().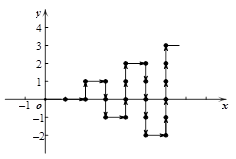
| A.( 14,0 ) | B.( 14,-1) | C.( 14,1 ) | D.( 14,2 ) |