甲、乙两地分别生产了17台、15台同一种型号的检测设备,全部运往A、B两个场馆.A场馆需要18台,B场馆需要14台,运往A、B两个场馆的运费如下表所示:
 |
甲地 |
乙地 |
| A场馆 |
800元/台 |
700元/台 |
| B场馆 |
500元/台 |
600元/台 |
(1)设甲地运往A场馆x台设备,写出总费用y(元)与x(台)之间的函数解析式;
(2)如果费用不高于20200元,有几种方案?
(3)当x为多少时,总费用最少?并求出最少总费用.
在如图所示的平面直角坐标系中描出A(2 3),B(-3,-2),C(4,1)三点,并用线段将A、B、C三点依次连接起来,你能求出它的面积吗?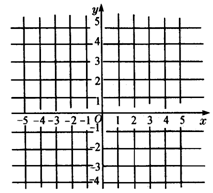
已知点A(a-1,2),B(-3,b+1),根据下列要求确定a、b的值:
(1)直线AB∥x轴.
(2)直线AB∥y轴.
(3)AB两点在第一、三象限的角平分线上.
在直角坐标系中设法找到若干个点,使得连结各点所得的封闭图形是如图所示的“+”字.
如图所示,是某市区部门简图,请你建立适当的坐标系,分别写出图中各地方的坐标.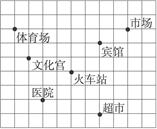
在直角坐标系中,标出下列各点的位置,并写出各点的坐标.
(1)点A在x轴上,位于原点的左侧,距离坐标原点4个单位长度;
(2)点B在y轴上,位于原点的上侧,距离坐标原点4个单位长度;
(3)点C在y轴的左侧,在x轴的上侧,距离每个坐标轴都是4个单位长度.
请大家在坐标纸上建立直角坐标系,并进行描点.