如图,在平面直角坐标系中，△ABC是直角三角形,∠ACB=90,AC=BC,OA=1，OC=4，抛物线y=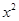
+bx+c经过A，B两点，抛物线的顶点为D．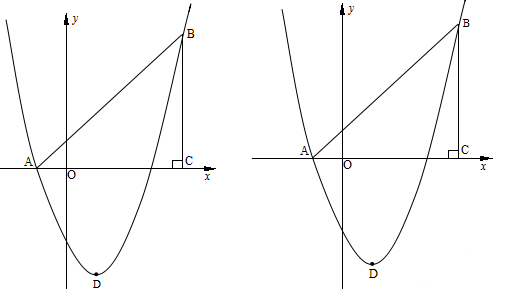
（1）求b,c的值；
（2）点E是直角三角形ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；
（3）在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形? 若存在，求出所有点P的坐标；若不存在，说明理由．
如图，AB为⊙O的直径，PQ切⊙O于E,AC⊥PQ于C，交⊙O于D.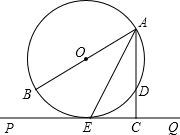
（1）求证：AE平分∠BAC;
（2）若AD=2，EC=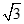
,∠BAC=600,求⊙O的半径.
如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于D，过D作DE⊥AC，交AC于E，求证：DE是⊙O的切线.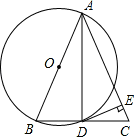
黄商超市以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件.超市为增加销售量，决定降价销售，根据市场调查，单价第降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，超市将对剩余的T恤一次性清仓销售，清仓时单价为40元，设第二个月单价降低x元.
（1）完成下表（不化简）
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价（元） |
80 |
40 |
|
| 销售量（件） |
200 |
（2）如果超市希望通过销售这批T恤获利9000元，那么第二个月的单价是多少元？
解下列方程(1)4x²-4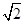
x+1=0
(2)(3x+2)²=（5-2x）²
已知，如图，在平面直角坐标系中，Rt△ABC的斜边BC在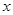
轴上，直角顶点A在
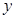轴的正半轴上，A（0，2），B（－1，0）。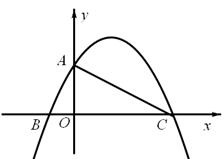
（1）求点C的坐标并求过A、B、C三点的抛物线的解析式
（2）设点P（m，n）是抛物线在第一象限部分上的点，△PAC的面积为S，求S关于m的函数关系式，并求使S最大时点P的坐标．；
（3）在抛物线的对称轴上是否存在点Q，使△QAC是以AC为腰的等腰三角形？如果存在，直接写出Q点的坐标；如果不存在，请说明理由；