已知数列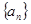 满足:
满足: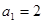 ,
,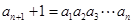 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)(ⅰ)证明:当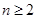 时,
时,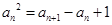 ;
;
(ⅱ)若正整数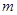 满足
满足 ,求
,求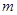 的值.
的值.
如图,要在一块半径为1m,圆心为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M、N在
OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.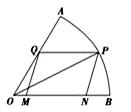
(1)求S关于θ的函数关系式;
(2)求S的最大值及相应θ的值.
已知二次函数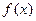 的二次项系数为a,且不等式
的二次项系数为a,且不等式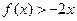 的解集为(1,3),
的解集为(1,3),
(1)若方程 有两个相等的根,求
有两个相等的根,求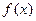 的解析式;
的解析式;
(2)若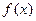 的最大值为正数,求a的取值范围;
的最大值为正数,求a的取值范围;
在锐角△ABC中,角A、B、C的对边长分别为a,b,c,已知b=5,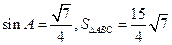 ,
,
(1)求边c的值;
(2)求sinC的值。
已知向量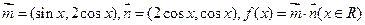 ,
,
(1)求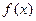 的最小正周期及对称中心;
的最小正周期及对称中心;
(2)求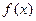 在
在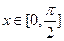 上的值域;
上的值域;
(3)令 ,若
,若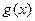 的图像关于原点对称,求
的图像关于原点对称,求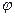 的值。
的值。
已知 ,
,
(1)求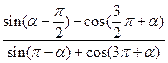 的值;(2)求
的值;(2)求 的值。
的值。