已知:抛物线y= +(2m-1)x+
+(2m-1)x+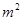 -1经过坐标原点,且当x<0时,y随x的增大而减小.
-1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B, DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为 (a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:吨/公顷):
| 品种 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
| 甲 |
9.8 |
9.9 |
10.1 |
10 |
10.2 |
| 乙 |
9.4 |
10.3 |
10.8 |
9.7 |
9.8 |
为使水稻品种的产量比较稳定,根据题中所给的数据,你选择哪种水稻品种?请说明理由.
如图,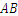 是⊙O的一条弦,
是⊙O的一条弦,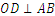 ,垂足为C,交⊙O于点D,点E在⊙O上.
,垂足为C,交⊙O于点D,点E在⊙O上.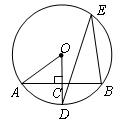
(1)若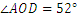 ,求
,求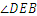 的度数;
的度数;
(2)若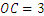 ,
,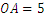 ,求
,求 的长.
的长.
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m。试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.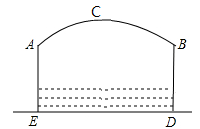
已知反比例函数 .
.
(1)画出该函数的大致图象。
(2)这个函数的大致图象位于哪些象限?函数值y随自变量x的增大如何变化?
解下列方程
(1)
(2)