甲、乙两种水稻试验品种连续5年的平均单位面积产量如下（单位：吨/公顷）：
| 品种 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
| 甲 |
9.8 |
9.9 |
10.1 |
10 |
10.2 |
| 乙 |
9.4 |
10.3 |
10.8 |
9.7 |
9.8 |
为使水稻品种的产量比较稳定，根据题中所给的数据，你选择哪种水稻品种？请说明理由.
如图1，四边形ABCD，AEFG都是正方形，E、G分别在AB、AD边上，已知AB=4．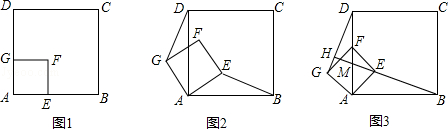
（1）求正方形ABCD的周长；
（2）将正方形AEFG绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，求证：BE=DG．
（3）将正方形AEFG绕点A逆时针旋转45°时，如图3，延长BE交DG于点H，设BH与AD的交点为M．
①求证：BH⊥DG；
②当AE=
时，求线段BH的长（精确到0．1）．
已知正比例函数y=x和反比例函数
的图象都经过点A（3，3）．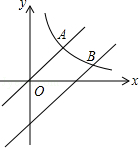
（1）直接写出反比例函数的解析式；
（2）把直线OA向下平移后与反比例函数的图象交于点B（6，m），求平移的距离．
已知一次函数y=kx+b的图象经过点（1，3）和点（2，5），求k和b的值．
如图，已知△ABC．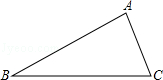
（1）作边BC的垂直平分线；
（2）作∠C的平分线．（要求：不写作法，保留作图痕迹）
①计算：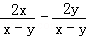
②解方程：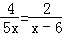
．