光滑水平面上有一质量为M="2" kg的足够长的木板,木板上最有右端有一大小可忽略、质量为m=3kg的物块,物块与木板间的动摩擦因数 ,且最大静摩擦力等于滑动摩擦力。开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P。现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且撞击时无动能损失,物块始终未能与挡板相撞,求:
,且最大静摩擦力等于滑动摩擦力。开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P。现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且撞击时无动能损失,物块始终未能与挡板相撞,求:
(1)木板第一次撞击挡板P时的速度 为多少?
为多少?
(2)木板从第一次撞击挡板P到运动至右端最远处所需的时间 及此时物块距木板右端的距离X为多少?
及此时物块距木板右端的距离X为多少?
(3)木板与挡板P会发生多次撞击直至静止,而物块一直向左运动。每次木板与挡板P撞击前物块和木板都已相对静止,最后木板静止于挡板P处,求木板与物块都静止时物块距木板最右端的距离X为多少?
一木箱静止在光滑水平地面上,装货物后木箱和货物的总质量为50kg.现以200N的水平推力推木箱,求:
(1)该木箱的加速度;
(2)第2s末木箱的速度。
质量为2吨的汽车在水平路面上做半径为40m的转弯,如果车速是36km/h,则:
(1)其所需的向心力多大?是由什么力提供的?
(2)若路面能提供的最大静摩擦力的值为车重的0.6倍,那么,若仍以36km/h速度转弯,转弯半径不小于多少m?(g取10m/s2)
一物体受到竖直向上的拉力F的作用,如图所示.当拉力F=42 N时,物体向上的加速度a=4.0 m/s2,不计空气阻力,g取10 m/s2.则: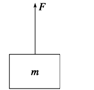
(1)物体的质量m为多大?
(2)物体由静止开始向上运动2 s内的位移和2 s末的速度分别为多少?
某人在距离地面2.6m的高处,将质量为0.2kg的小球以v0=12m/s速度斜向上抛出,小球的初速度方向与水平方向之间的夹角为30º,g取10m/s2,求:
(1)人抛球时对球做多少功?
(2)若不计空气阻力,小球落地时的速度大小是多少?
(3)若小球落地时的速度大小为v1=13m/s,小球在空中运动过程中克服阻力做了多少功?
一长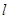 =0.80m的轻绳一端固定在
=0.80m的轻绳一端固定在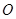 点,另一端连接一质量
点,另一端连接一质量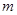 =0.10kg的小球,悬点
=0.10kg的小球,悬点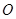 距离水平地面的高度H = 1.00m.开始时小球处于
距离水平地面的高度H = 1.00m.开始时小球处于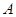 点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到
点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到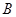 点时,轻绳碰到悬点
点时,轻绳碰到悬点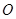 正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.
正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2. 
(1)绳断裂后球从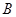 点抛出并落在水平地面的C点,求C点与
点抛出并落在水平地面的C点,求C点与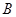 点之间的水平距离.
点之间的水平距离.
(2)若轻绳所能承受的最大拉力Fm = 9.0N,求钉子P与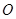 点的距离d应满足什么条件?
点的距离d应满足什么条件?