(本小题满分12分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,△APB面积的最大值为2 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线AP的倾斜角为 ,且与椭圆在点B处的切线交于点D,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
,且与椭圆在点B处的切线交于点D,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
设甲、乙、丙三人进行围棋比赛,每局两人参加,没有平局。在一局比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。
。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。
(1)求只进行了三局比赛,比赛就结束的概率;
(2)记从比赛开始到比赛结束所需比赛的局数为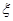 ,求
,求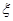 的概率分布列和数学期望
的概率分布列和数学期望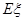 。
。
已知向量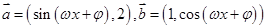 ,
, ,函数
,函数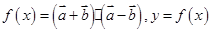 图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点
图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点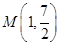 。
。
(1)求函数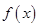 的解析式
的解析式
(2)当 时,求函数
时,求函数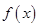 的单调区间。
的单调区间。
已知函数 .(
.( )
)
(1)当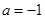 时,试确定函数
时,试确定函数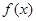 在其定义域内的单调性;
在其定义域内的单调性;
(2)求函数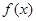 在
在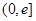 上的最小值;
上的最小值;
(3)试证明: .
.
已知数列 满足
满足 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(3)设 ,记
,记 ,证明:
,证明: .
.
已知椭圆 (a>b>0)的离心率为
(a>b>0)的离心率为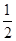 ,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+
,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+ 相切.
相切.
(1)求椭圆的方程;
(2)设直线 与椭圆在
与椭圆在 轴上方的一个交点为
轴上方的一个交点为 ,
, 是椭圆的右焦点,试探究以
是椭圆的右焦点,试探究以 为
为
直径的圆与以椭圆长轴为直径的圆的位置关系.