自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0.不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正常数a,b,c.
(Ⅰ)求xn+1与xn的关系式;
(Ⅱ)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
(Ⅲ)设a=2,b>0,c=1为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的最大允许值是多少?证明你的结论.
如图,已知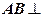 平面
平面 ,
, 平面
平面 ,
,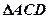 为等边三角形,
为等边三角形,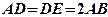 ,
, 为
为 中点.
中点.
(1)求证: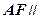 平面
平面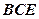 ;
;
(2)求证:平面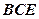
 平面
平面 ;
;
(3)求直线 与平面
与平面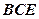 所成角的正弦值.
所成角的正弦值.
已知向量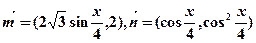 .
.
(1)若 ,求
,求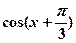 的值;
的值;
(2)记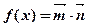 ,在
,在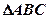 中,角
中,角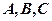 的对边分别为
的对边分别为 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
已知数列 是首项为1的等差数列,且
是首项为1的等差数列,且 ,若
,若 成等比数列,(1)求数列
成等比数列,(1)求数列 的通项公式;(2)设
的通项公式;(2)设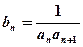 ,求数列
,求数列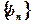 的前
的前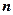 项和
项和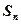 .
.
(选修4-5:不等式选讲)
关于 的不等式
的不等式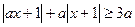 ,
,
(1)当 时,解上述不等式;
时,解上述不等式;
(2)当 时,若上述不等式恒成立,求实数
时,若上述不等式恒成立,求实数 的取值范围。
的取值范围。
(选修4-4:坐标系与参数方程)
已知极坐标系的极点O与直角坐标系的原点重合,极轴与 轴的正半轴重合,曲线
轴的正半轴重合,曲线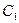 :
: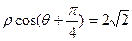 与曲线
与曲线 交于A、B两点。
交于A、B两点。
(1)证明:OA⊥OB;(2)求弦长|AB|。