已知数列 是首项为1的等差数列,且
是首项为1的等差数列,且 ,若
,若 成等比数列,(1)求数列
成等比数列,(1)求数列 的通项公式;(2)设
的通项公式;(2)设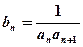 ,求数列
,求数列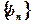 的前
的前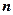 项和
项和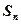 .
.
利民商店经销某种洗衣粉,年销售量为6000包,每包进价2.80元,销售价3.40元,全年分若干次进货,每次进货x包,已知每次进货运输劳务费62.50元,全年保管费为1.5x元。
(1)把该商店经销洗衣粉一年的利润y(元)表示为每次进货量x(包)的函数,并指出函数的定义域;
(2)为了使利润最大,每次应该进货多少包?
设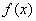 是定义在
是定义在 上的单调增函数,满足
上的单调增函数,满足 ,
,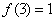 ;
;
(1)求 ;
;
(2)若 ,求
,求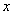 的取值范围。
的取值范围。
已知 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,  。
。
(1)用分段函数形式写出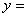
 在
在 上的解析式;
上的解析式;
(2)画出函数 的大致图象;并根据图像写出
的大致图象;并根据图像写出 的单调区间;
的单调区间;
已知U=R,A={ ||
|| -3|<2
-3|<2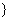 , B={
, B={ |
| >0},
>0},
求A∩B, C (A∪B) 。
(A∪B) 。
(本小题满分8分)
某商店经营的消费品进价每件14元,月销售量 (百件)与销售价格
(百件)与销售价格 (元)的关系如下图,每月各种开支2000元.
(元)的关系如下图,每月各种开支2000元.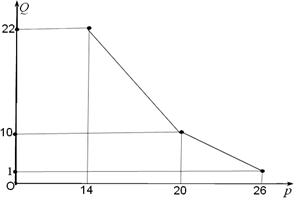
(1)写出月销售量 (百件)与销售价格
(百件)与销售价格 (元)的函数关系;
(元)的函数关系;
(2)写出月利润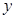 (元)与销售价格
(元)与销售价格 (元)的函数关系;
(元)的函数关系;
(3)当商品价格每件为多少元时,月利润最大?并求出最大值.