已知 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,  。
。
(1)用分段函数形式写出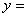
 在
在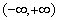 上的解析式;
上的解析式;
(2)画出函数 的大致图象;并根据图像写出
的大致图象;并根据图像写出 的单调区间;
的单调区间;
【2015高考北京,文17】(本小题满分13分)某超市随机选取 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,
整理成如下统计表,其中“√”表示购买,“×”表示未购买.
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买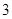 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
【2015高考安徽,文17】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
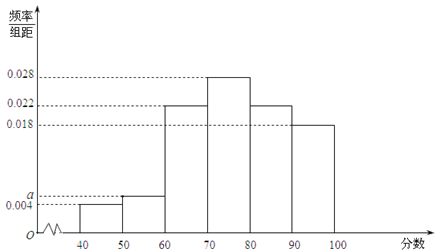
(Ⅰ)求频率分布图中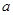 的值;
的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在 的概率.
的概率.
【2015高考上海,文19】如图,圆锥的顶点为 ,底面的一条直径为
,底面的一条直径为 ,
, 为半圆弧
为半圆弧 的中点,
的中点, 为劣弧
为劣弧 的中点.已知
的中点.已知 ,
,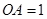 ,求三棱锥
,求三棱锥 的体积,并求异面直线
的体积,并求异面直线 与
与 所成角的大小.
所成角的大小.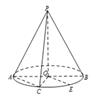
【2015高考重庆,文20】如图,三棱锥P-ABC中,平面PAC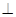 平面ABC,
平面ABC, ABC=
ABC= ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB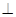 平面PFE.
平面PFE.
(Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.
【2015高考浙江,文18】如图,在三棱锥 中,
中, 在底面ABC的射影为BC的中点,D为
在底面ABC的射影为BC的中点,D为 的中点.
的中点.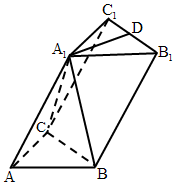
(1)证明: ;
;
(2)求直线 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.