如图,在几何体 中,
中, 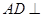 平面
平面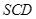 ,
,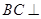 平面
平面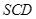 ,
,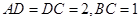 ,又
,又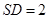 ,
,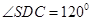 .
.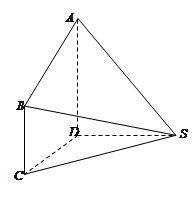
(1)求 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
设椭圆C1: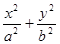 =1(a>b>0)的左、右焦点分别为为
=1(a>b>0)的左、右焦点分别为为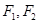 ,
,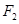 恰是抛物线C2:
恰是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
的焦点,点M为C1与C2在第一象限的交点,且|MF2|= .
.
(1)求C1的方程;
(2)平面上的点N满足 ,直线l∥MN,且与C1交于A,B两点,若
,直线l∥MN,且与C1交于A,B两点,若 ,求直线l的方程.
,求直线l的方程.
某地为迎接2014年索契冬奥会,举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛,其得分情况如茎叶图所示: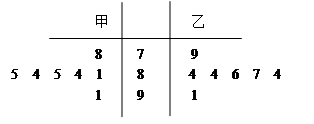
(1)若从甲运动员的不低于80且不高于90的得分中任选3个,求其中与平均得分之差的绝对值不超过2的概率;
(2)若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个,求甲、乙两名运动员得分之差的绝对值 的分布列与期望.
的分布列与期望.
在如右图的几何体中,四边形 为正方形,四边形
为正方形,四边形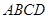 为等腰梯形,
为等腰梯形,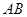 ∥
∥ ,
, ,
, ,
,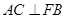 .
.
(1)求证: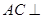 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.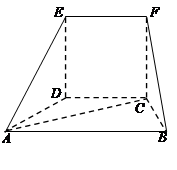
数列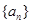 的前
的前 项和为
项和为 ,且
,且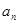 是
是 和
和 的等差中项,等差数列
的等差中项,等差数列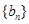 满足
满足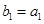 ,
, .
.
(1)求数列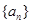 、
、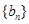 的通项公式;
的通项公式;
(2)设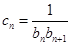 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
在无穷数列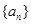 中,
中, ,对于任意
,对于任意 ,都有
,都有 ,
, . 设
. 设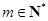 , 记使得
, 记使得 成立的
成立的 的最大值为
的最大值为 .
.
(1)设数列 为1,3,5,7,
为1,3,5,7,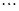 ,写出
,写出 ,
, ,
,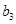 的值;
的值;
(2)若 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列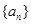 ;
;
(3)设 ,
,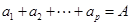 ,求
,求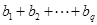 的值.(用
的值.(用 表示)
表示)