如图,在平面直角坐标系中,抛物线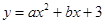 与
与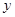 轴交于点C,与
轴交于点C,与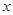 轴交于点A(
轴交于点A( ,0),B(
,0),B(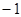 ,0).
,0).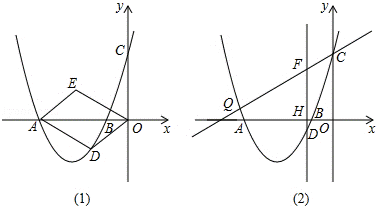
(1)求抛物线的解析式;
(2)在第三象限的抛物线上有一动点D.
①如图(1),若四边形ODAE是以OA为对角线的平行四边形,当平行四边形ODAE的面积为6时,请判断平行四边形ODAE是否为菱形?说明理由.
②如图(2),直线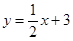 与抛物线交于点Q、C两点,过点D作直线DF⊥
与抛物线交于点Q、C两点,过点D作直线DF⊥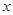 轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与点C到直线DF的距离之比为
轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与点C到直线DF的距离之比为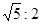 ?若存在,请求出点D的坐标;若不存在,请说明理由.
?若存在,请求出点D的坐标;若不存在,请说明理由.
上海世博会自2010年5月1日起到10月31日止,历时184天.2010年5月21日小红根据前10天的入园人数制作了如下统计图.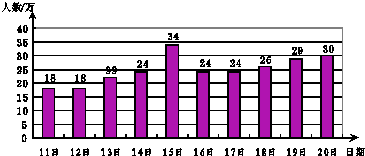
(1)请根据统计图所提供的信息填空:这十天入园人数的众数为万人,中位数为万人,极差为万人;
(2)根据统计图所提供的数据,估算世博会期间入园的总人数?
(3)据中国2010年上海世博会官方网统计,世博会期间实际入园总人数为7308万人,求实际入园总人数比估算入园总人数多多少万人?并分析:在利用小红所提供的样本估计入园总人数时,产生较大偏差的原因是什么?
要了解某地区九年级学生的身高情况,从中随机抽取150名学生的身高作为一个样本,身高均在141cm~175cm之间(取整数厘米),整理后分成7组,绘制出频数分布直方图(不完整).根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)该地区共有3000名九年级学生,估计其中身高不低于161cm的人数;
(3)估计该地区九年级学生身高不低于151cm的概率.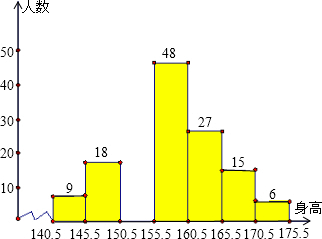
某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到六年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到六年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
| 类别 |
频率(人数) |
频率 |
| 武术类 |
0.25 |
|
| 书画类 |
20 |
0.2 |
| 棋牌类 |
15 |
b |
| 器乐类 |
||
| 合计 |
a |
1 |
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
①a=,b=;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是;
③若该校六年级有学生560人,请你估计大约有多少学生参加武术类校本课程.
水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为 米,加固后大坝的横截面积为梯形ABED,CE的长为8米.
米,加固后大坝的横截面积为梯形ABED,CE的长为8米.
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE的坡度.
如图,一艘货轮在A处发现其北偏东45°方向有一海盗船,立即向位于正东方向B处的海警舰发出求救信号,并向海警舰靠拢,海警舰立即沿正西方向对货轮实施救援,此时距货轮200海里,并测得海盗船位于海警舰北偏西60°方向的C处.
(1)求海盗船所在C处距货轮航线AB的距离.
(2)若货轮以45海里/时的速度在A处沿正东方向海警舰靠拢,海盗以50海里/时的速度由C处沿正南方向对货轮进行拦截,问海警舰的速度应为多少时才能抢在海盗之前去救货轮?(结果保留根号)