已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).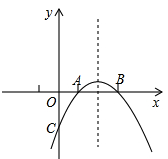
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
先化简,再求值:  ,其中
,其中 
计算:
荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
阅读理解题:
阅读例子:已知:关于 、
、 的方程组
的方程组 的解是
的解是 ,
,
求关于 、
、 的方程组
的方程组 的解.
的解.
解:方程组 可化为
可化为
∵方程组 的解是
的解是 ,∴
,∴ ∴
∴ 
∴ 方程组 的解是
的解是
通过对上面材料的认真阅读后,解方程组:已知:关于 、
、 的方程组
的方程组
的解是 ,求关于
,求关于 、
、 的方程组
的方程组 的解.
的解.
京津城际铁路将于2008年8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米?