(阅读)如图1,在平面直角坐标系xoy中,已知点A(a、O)(a>0),B(2,3),C(0,3)。过原点O作直线l,使它经过第一、第三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
【理解】若点D与点A重合,则这个操作过程为FZ[ , ];直接写出答案
【尝试】
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(6分)如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
如图1,在平面直角坐标系中, 为坐标原点.直线
为坐标原点.直线 与抛物线
与抛物线 同时经过
同时经过 .
.
(1)求 的值.
的值.
(2)点 是二次函数图象上一点,(点
是二次函数图象上一点,(点 在
在 下方),过
下方),过 作
作
 轴,与
轴,与 交于点
交于点 ,与
,与 轴交于点
轴交于点 .求
.求 的最大值.
的最大值.
(3)在(2)的条件下,是否存在点 ,使
,使 和
和  相似?若存在,求出
相似?若存在,求出 点坐标,不存在,说明理由.
点坐标,不存在,说明理由.
 中,AB=AC,将线段AB绕点A按逆时针方向旋转
中,AB=AC,将线段AB绕点A按逆时针方向旋转 得到线段AD,其中
得到线段AD,其中 .连结BD,CD,
.连结BD,CD,  .
.
(1)若 ,
, ,在图1中补全图形,并写出m值.
,在图1中补全图形,并写出m值.
(2)如图2,当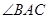 为钝角,
为钝角, 时 ,
时 , 值是否发生改变?证明你的猜想.
值是否发生改变?证明你的猜想.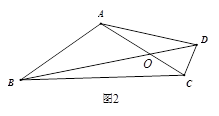
(3) 如图3,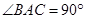 ,
, ,BD与AC相交于点O,求
,BD与AC相交于点O,求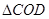 与
与 的面积比.
的面积比.
在平面直角坐标系 中,抛物线
中,抛物线 的开口向下,且抛物线与
的开口向下,且抛物线与 轴的交于点
轴的交于点 ,与
,与 轴交于
轴交于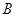 ,
, 两点,(
两点,(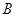 在
在 左侧). 点
左侧). 点 的纵坐标是
的纵坐标是 .
.
(1)求抛物线的解析式;
(2)求直线 的解析式;
的解析式;
(3)将抛物线在点 左侧的图形(含点
左侧的图形(含点 )记为
)记为 .若直线
.若直线 与直线
与直线 平行,且与
平行,且与
图形 恰有一个公共点,结合函数图象写出
恰有一个公共点,结合函数图象写出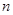 的取值范围.
的取值范围.
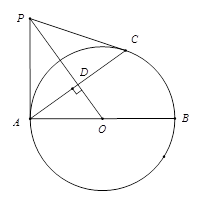
如图,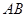 是
是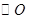 的直径,
的直径,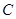 是圆周上一点,
是圆周上一点,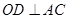 于点
于点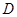 .
.
过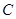 作
作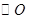 的切线,交
的切线,交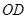 的延长线于点
的延长线于点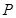 ,连接
,连接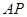 .
.
(1)求证: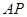 是
是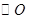 的切线.
的切线.
(2)若 ,
,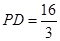 ,求
,求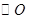 的半径.
的半径.