某所学校位于北纬21°，此地一年中冬至日正午时刻，太阳光与地面的夹角最小，约为35．5°；夏至日正午时刻，太阳光的夹角最大，约为82．5°．己知该校一教学楼窗户朝南，窗高207cm，如图（1）．请你为该窗户设计一个直角形遮阳棚BCD，如图（2），要求最大限度地节省材料，夏至日正午刚好遮住全部阳光，冬至日正午能射入室内的阳光没有遮挡．
（1）在图（3）中画出设计草图；
（2）求BC、CD的长度（结果精确到个位）
（参考数据：sin35．5°≈0．58，cos35．5°≈0．81，tan35．5°≈0．71，sin82．5°≈0．99，cos82．5°≈0．13，tan82．5°≈7．60）
图①、图②都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在每个网格中标注了5个格点．按下列要求画图：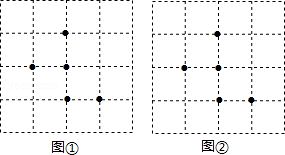
（1）在图①中以格点为顶点画一个等腰三角形，使其内部已标注的格点只有3个；
（2）在图②中，以格点为顶点，画一个正方形，使其内部已 标注的格点只有3个，且边长为无理数．
临川一中要从甲、乙两位男生和丙、丁两位女生中选派两名同学代表学校参加全区汉字听写大赛。
（1）用树状图或者列表法列举出所有可能选派的结果。
（2）求恰好选派一男一女两位同学参赛的概率。
如图，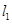
∥
∥
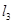，AB=3，BC=5，DF=12，求DE和EF的长。
若∣m∣=1，求关于x的一元二次方程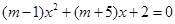
的解。
如图，平面直角坐标系中，直线AB：y=-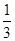
x+b交y轴于点A（0，1），交x轴于点B．直线x=1交AB于点D，交x轴于点E，P是直线x=1上一动点，且在点D的上方，设P（1，n）．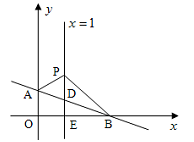
（1）求直线AB的解析式和点B的坐标；
（2）求△ABP的面积（用含n的代数式表示）；
（3）当S△ABP=2时，以PB为边在第一象限作等腰直角三角形BPC，求出点C的坐标．（考虑问题要全面哦……）