若关于x的二次函数y=a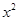
+bx+c（a＞0，c＞0，a、b、c是常数）与x轴交于两个不同的点A（
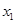，0），B（
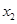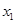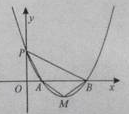
，0）（0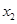＜＜），与y轴交于点P，其图像顶点为点M，点O为坐标原点。
（1）当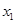=c=2，a=
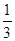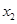时，求与b的值；
（2）当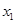=2c时，试问△ABM能否为等边三角形？判断并证明你的结论；
（3）当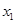=mc（m＞0）时，记△MAB，△PAB的面积分别为S1，S2，若△BPO∽△PAO，且S1=S2,求m的值。
|
先化简，后求值：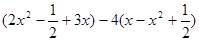
，其中
.
如左下图所示用5个棱长1厘米的小立方体块搭成的几何体，请画出它的主视图、俯视图与左视图.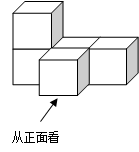
计算：
（1）（–2）2–（1–0.8×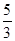
）÷（–2）
（2）
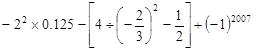
某校为了了解九年级学生的体能情况，抽调了一部分学生进行一分钟跳绳测试，将测试成绩整理后作出如下统计图．甲同学计算出前两组的频率和是0.12，乙同学计算出跳绳次数不少于100次的同学占96％，丙同学计算出从左至右第二.三.四组的频数比为4∶17∶15．结合统计图回答下列问题：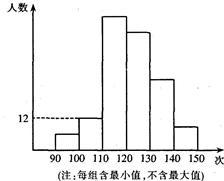
（1）这次共抽调了多少人?
（2）若跳绳次数不少于130次为优秀，则这次测试成绩的优秀率是多少?
下图表示的是某班同学衣服上口袋的数目：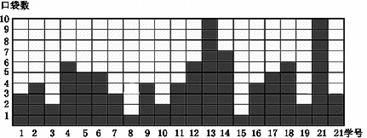
（1）从图中是否能够得出以下信息？
①只有4个人的衣服上有4个口袋；
②只有1个人的衣服上有8个口袋；
③只有3个人的衣服上有5个口袋；
（2）根据上图填写下面的频数分布表，并绘制频数分布直方图.
| 口袋数目 |
1≤x＜3 |
3≤x＜5 |
5≤x＜7 |
7≤x＜9 |
x≥9 |
| 频数记录 |
|||||
| 频数 |