（本小题满分12分）如图，在平面直角坐标系xOy中，抛物线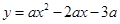
（
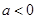）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：
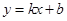与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．
（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；
（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为
，求a的值；
（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．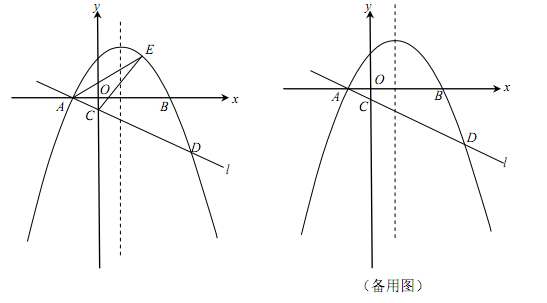
（本题8分）如图，△ABO≌△CDO，点B在CD上，AO∥CD，∠BOD＝30°，求∠A的度数．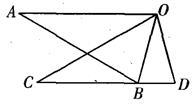
（本题7分）如图，点B、C在∠SAT的两边上，且AB＝AC．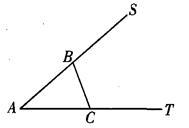
（1）请按下列语句用尺规画出图形．（不写画法，保留作图痕迹）
①AN⊥BC，垂足为N；
②∠SBC的平分线交AN延长线于点M；
③连接CM．
（2）该图中有_______对全等三角形．
（本题6分） 如图，在△ABC中，∠ACB=90，AC=BC．直线L经过点C且绕点C转动，分别过点A、B向直线DE引垂线，垂足分别为点D、E．
求证：AD+BE=DE．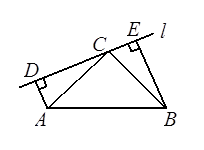
（本题6分）如图，点E、C在线段BF上，BE=CF，AB∥DE，∠ACB=∠F，那么△ABC与△DEF全等吗?为什么?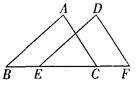
（本题6分）下列图形是否是轴对称图形，画出轴对称图形的所有对称轴．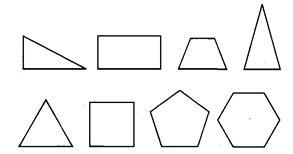
思考：正三角形有_______条对称轴；正四边形有______条对称轴；正五边形有_______条对称轴；正六边形有_______条对称轴；正n边形有_______条对称轴．
当n越来越大时，正多边形接近于什么图形？它有多少条对称轴？