(本小题满分13分)已知函数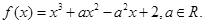
(1)当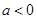 时,求函数
时,求函数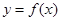 的单调区间;
的单调区间;
(2)若 ,且曲线
,且曲线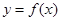 在点
在点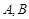 (
(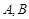 不重合)处切线的交点位于直线
不重合)处切线的交点位于直线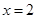 上,求证:
上,求证: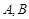 两点的横坐标之和小于4;
两点的横坐标之和小于4;
(3)当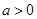 时,如果对于任意
时,如果对于任意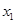 、
、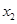 、
、 ,
, ,总存在以
,总存在以 、
、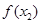 、
、 为三边长的三角形,试求实数
为三边长的三角形,试求实数 的取值范围.
的取值范围.
(本小题满分12分)
如图,四边形ABCD是平面图形,BC=CD=1,AB=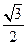 BD,
BD, 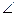 ABD=
ABD= ,设
,设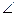 BCD=
BCD= ,四边形ABCD的面积为S,求函数S=
,四边形ABCD的面积为S,求函数S= 的最大值.
的最大值.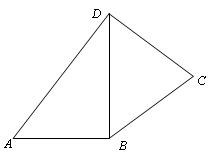
设函数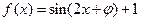 (
( )过点
)过点 .
.
(1)求函数 的值域;
的值域;
(2)用五点法画出函数 在一个周期上的图象(要求列表).
在一个周期上的图象(要求列表).
(本小题满分12分)
(1)已知 ,求
,求 的值;
的值;
(2)已知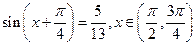 求
求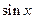 的值.
的值.
已知函数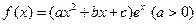 的图象在点
的图象在点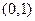 处的切线的斜率为
处的切线的斜率为 ,且在
,且在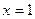 处取得极小值。
处取得极小值。
(1)求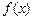 的解析式;
的解析式;
(2)已知函数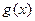 定义域为实数集
定义域为实数集 ,若存在区间
,若存在区间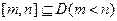 ,使得
,使得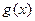 在
在 的值域也是
的值域也是 ,称区间
,称区间 为
为 函数
函数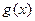 的“保值区间”.
的“保值区间”.
①当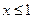 时,请写出函数
时,请写出函数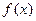 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明);
②当 时,问
时,问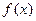 是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
某企业生产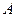 产品,拟开发新产品
产品,拟开发新产品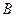 ,根据市场调查与预测,
,根据市场调查与预测,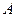 产品的利润与投资额关系成正比例关系,如图一;若投资
产品的利润与投资额关系成正比例关系,如图一;若投资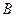 产品,至少需要
产品,至少需要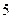 万元,其利润与投资额关系为
万元,其利润与投资额关系为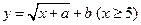 ,如图二.(单位:万元)
,如图二.(单位:万元)
(1)分别将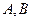 两种产品的利润
两种产品的利润 表示为投资金额
表示为投资金额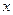 的函数关系式;
的函数关系式;
(2)该企业已筹集到 万元资金
万元资金 ,并全部投入两种产品的生产,问:怎样分配这
,并全部投入两种产品的生产,问:怎样分配这 万元投资,才能使企业获得最大利润?其最大利润约为多少万元?
万元投资,才能使企业获得最大利润?其最大利润约为多少万元? 