已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆C的标准方程
(2)若直线L:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点D.求证:直线L过定点,并求处该定点的坐标。
(本小题满分12分)已知函数 .
.
(Ⅰ)若函数 在
在 单调递增,求
单调递增,求 取值范围;
取值范围;
(Ⅱ)若函数 的最小值为0,且当
的最小值为0,且当 时,
时,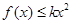 ,求
,求 的最小值.
的最小值.
(本小题满分12分)已知抛物线C: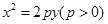 的焦点为F,直线
的焦点为F,直线 与
与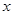 轴的交点为P,与C的交点为Q,且
轴的交点为P,与C的交点为Q,且 .
.
(Ⅰ)求C的方程;
(Ⅱ)点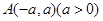 在抛物线C上,是否存在直线
在抛物线C上,是否存在直线 与C交于点
与C交于点 ,使得△
,使得△ 是以
是以 为斜边的直角三角形?若存在,求出直线
为斜边的直角三角形?若存在,求出直线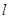 的方程;若不存在说明理由.
的方程;若不存在说明理由.
(本小题满分12分)如图,直三棱柱 中,
中, ,
, 是棱
是棱 的中点,
的中点, .
.
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 的大小.
的大小.
(本小题满分12分)砷是广泛分布于自然界中的非金属元素, 长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位: ):
): 
甲地区的10个村子饮用水中砷的含量:
52 32 41 72 43 35 45 61 53 44
乙地区的10个村子饮用水中砷的含量:
44 56 38 61 7257 64 71 58 62
(Ⅰ)根据两组数据完成下面茎叶图,试比较两个地区中哪个地区的饮用水中砷含量更高,并说明理由;
(Ⅱ)国家规定居民饮用水中砷的含量不得超过50 ,现医疗卫生组织决定向两个地区中每个砷超标的村子派驻一个医疗救助小组.用样本估计总体,把频率作为概率,若从乙地区随机抽取3个村子,用
,现医疗卫生组织决定向两个地区中每个砷超标的村子派驻一个医疗救助小组.用样本估计总体,把频率作为概率,若从乙地区随机抽取3个村子,用 表示派驻的医疗小组数,试写出
表示派驻的医疗小组数,试写出 的分布列并求
的分布列并求 的期望.
的期望.
(本小题满分12分)已知函数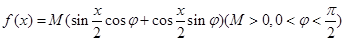 的最大值是2,且
的最大值是2,且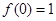 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)已知锐角△ 的内角
的内角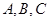 的对边分别为
的对边分别为 ,若
,若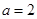 ,
, ,
, .求△
.求△ 的面积.
的面积.