设函数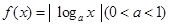 的定义域为
的定义域为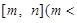
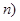 ,值域为
,值域为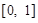 ,若
,若 的最小值为
的最小值为 ,则实数a的值为( )
,则实数a的值为( )
A. |
B. 或 或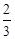 |
C.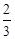 |
D.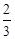 或 或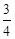 |
给出下列三个命题:
①函数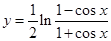 与
与 是同一函数;
是同一函数;
②若函数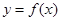 与
与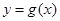 的图像关于直线
的图像关于直线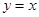 对称,则函数
对称,则函数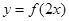
与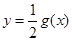 的图像也关于直线
的图像也关于直线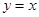 对称;
对称;
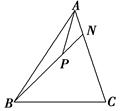
③如图,在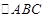 中,
中,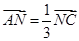 ,
,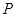 是
是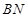 上的一点,若
上的一点,若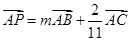 ,则实数
,则实数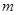 的值为
的值为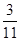 .
.
其中真命题是
| A.①② | B.①③ | C.②③ | D.② |
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有 ( )
| A.0个 | B.1个 | C.2个 | D.3个 |
将函数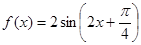 的图像向右平移
的图像向右平移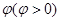 个单位,再将图像上每一点横坐标缩短到原来的
个单位,再将图像上每一点横坐标缩短到原来的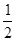 倍,所得图像关于直线
倍,所得图像关于直线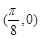 对称,则
对称,则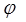 的最小正值为( )
的最小正值为( )
A.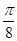 |
B.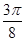 |
C. |
D.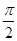 |
若定义在R上的偶函数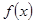 满足
满足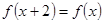 且
且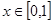 时,
时, 则方程
则方程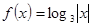 的零点个数是( )
的零点个数是( )
| A.2个 | B.3个 | C.4个 | D.多于4个 |