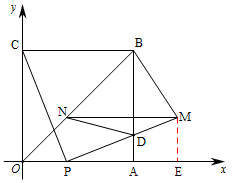
（本小题满分10分）如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连结CP，过点P作PM⊥CP交AB于点D，且PM＝CP，过点M作MN∥OA，交BO于点N，连结ND、BM，设OP＝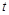
．
（1）求点M的坐标（用含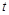的代数式表示）；
（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由；
（3）当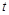为何值时，四边形BNDM的面积最小．
(8分)有一些写有数字的卡片，按序排列：第一张数字为－1，以后的每一张卡片上的数都是前一张卡片上的数的绝对值加1，且符号相反。即：－1，2，－3，4，－5，6 ……
⑴小华从中拿出相邻的3张卡片，若这些卡片上的数和为7，那么小华拿到的3张卡片为。
⑵你能拿到相邻的3张卡片，使得这些卡片上的数之和为2012吗？并请说明理由。
(6分)张新和李明到图书城去买书,请你根据他们的对话内容(如图),求出李明上次所买书籍的原价.
(8分)（1）利用网格线画图：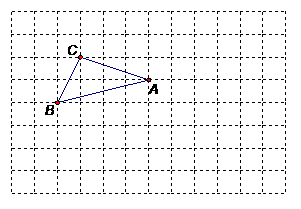
①过点A画AM⊥AC．
②将△ABC绕点A旋转180°，画出旋转后的图形．
（要在图中标出相关的点保留画图痕迹）
（2）小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分)，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子．
注意：只需添加一个符合要求的正方形，并用阴影表示．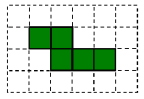
(8分)已知OC是
内部的一条射线，M、N分别为OA、OB上的点，线段OM、ON分别以20°/s、10°/s的速度绕点O逆时针旋转。
（1）如图①，若
，当OM、ON逆时针旋转2s时，分别到OM′、ON′处，
求
的值；
（2）如图②，若OM、ON分别在
、
内部旋转时，总有
，
求
的值。
下列图表是某校今年参加中考体育的男生1000米跑、女生800米跑的成绩中分别抽取的10个数据．
| 考生 编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 男生 成绩 |
3′05〞 |
3′11〞 |
3′53〞 |
3′10〞 |
3′55〞 |
3′30〞 |
3′25〞 |
3′19〞 |
3′27〞 |
3′55〞 |
（1）求出这10名女生成绩的中位数、众数；
（2）按《娄底市中考体育测试》规定，女生800米跑成绩不超过3′38 〞就可以得满分．该校学生有490人，男生比女生少70人． 请你根据上面抽样的结果，估算该校考生中有多少名女生该项考试得满分？
（3）若男考生1号和10号同时同地同向围着400米跑道起跑，在1000米的跑步中，他们能否首次相遇？如果能相遇，求出所需时间；如果不能相遇，说明理由．