如图，在平面直角坐标系中，直角三角形AOB的顶点A、B分别落在坐标轴上．O为原点，点A的坐标为（6，0），点B的坐标为（0，8）．动点M从点O出发．沿OA向终点A以每秒1个单位的速度运动，同时动点N从点A出发，沿AB向终点B以每秒
个单位的速度运动．当一个动点到达终点时，另一个动点也随之停止运动，设动点M、N运动的时间为t秒（t＞0）．
（1）当t=3秒时．直接写出点N的坐标，并求出经过O、A、N三点的抛物线的解析式；
（2）在此运动的过程中，△MNA的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由；
（3）当t为何值时，△MNA是一个等腰三角形？
（1）计算：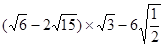
(2)解方程组：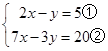
某蔬菜经销商到蔬菜种植基地采购一种蔬菜，经销商一次性采购蔬菜的采购单价y（元/千克）与采购量x（千克）之间的函数关系图象如图中折线AB——BC——CD所示（不包括端点A）．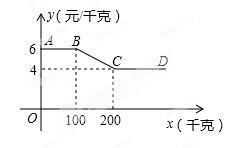
（1）当100＜x＜200时，直接写y与x之间的函数关系式．
（2）蔬菜的种植成本为2元/千克，某经销商一次性采购蔬菜的采购量不超过200千克，当采购量是多少时，蔬菜种植基地获利最大，最大利润是多少元？
如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，如果∠ACD=45°，⊙O的半径是4cm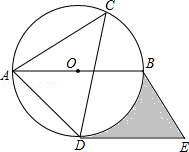
（1）请判断DE与⊙O的位置关系，并说明理由；
（2）求图中阴影部分的面积（结果用π表示）．
如图，为了测出某塔CD的高度，在塔前的平地上选择一点A，用测角仪测得塔顶D的仰角为30°，在A、C之间选择一点B（A、B、C三点在同一直线上）．用测角仪测得塔顶D的仰角为75°，且AB间的距离为40m．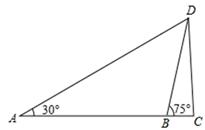
（1）求点B到AD的距离；
（2）求塔高CD（结果用根号表示）．
四张小卡片上分别写有数字1、2、3、4，它们除数字外没有任何区别，现将它们放在盒子里搅匀．
（1）随机地从盒子里抽取一张，求抽到数字3的概率；
（2）随机地从盒子里抽取一张，将数字记为
，不放回再抽取第二张，将数字记为
，请你用画树状图或列表的方法表示所有等可能的结果，并求出点（x，y）在函数
图象上的概率．