如图，矩形ABCD中，P是边AD上的一动点，连接BP、CP，过点B作射线交线段CP的延长线于点E，交AD边于点M，且使得∠ABE=∠CBP，如果AB=2，BC=5，AP=x，PM=y.
（1）说明△ABM∽△APB；并求出y关于x的函数关系式，写出自变量x的取值范围；
（2）当AP=4时，求sin∠EBP的值；
（3）如果△EBC是以∠EBC为底角的等腰三角形，求AP的长。
（1）计算：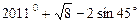
；
（2）解分式方程：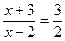
.
已知抛物线y＝ax2＋bx＋c与直线y＝mx＋n相交于两点，这两点的坐标分别是（0,
）和
（m－b，m2－mb＋n），其中a，b，c
，m，n为实数,且a，m不为0．
（1）求c的值；
（2）设抛物线y＝ax2＋bx＋c与x轴的两个交点是（x1，0）和（x2，0），求x1x2的值；
（3）当－1≤x≤1时，设抛物线y＝ax2＋bx＋c上与x轴距离最大的点为P（xo，yo），求这时｜yo｜的最小值．
如图1，Rt△ABC两直角边的边长为AC＝1，BC＝2．
（1）如图2，
⊙O与Rt△ABC的边AB相切于点X，与边CB相切于点Y．请你在图2中作出并标明⊙O的圆心O；（用尺规作图，保留作图痕迹，不写作法和证明）
（2）P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切．设⊙P的面积为s，你认为能否确定s的最大值？若能，请你
求出s的最大值;若不能,请你说明不能确定s的最大值的理由．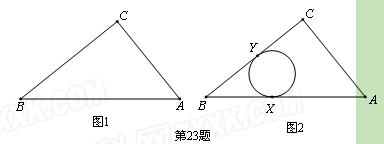
随着经济的发展，尹进所在的公司每年
都在元月一次性的提高员工当年的月工资。尹进2008年的月工资为2000元，在2010年时他的月工资增加到2420元，他2011年的月工资按2008到2010年的月工资的平均增长率继续增长．
（
1）尹进2011年的月工资为多少?
（2）尹进看了甲、乙两种
工具书的单价，认为用自己2011年6月份的月工资刚
好购买若干本甲种工具书和一些乙种工具书，当他拿着选定的这些工具书去付书款时，发现自己计算书款时把这两种工具书的单价弄对换了，故实际付款比2011年6月份的月工资少了242元，于是他用这242元又购买了甲、乙两种工具书各一本，并把购买的这两种工具书全部捐献给西部山区的学校．请问，尹进总共捐献了多少本工具书？
如图，D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF，E为垂足，EF与AB的延长线相交于点F，点O在AD上，AO＝CO，BC∥EF．
(1)证明：AB＝AC；
(2)证明：点O是△ABC的外接圆的圆心；
(3)当AB＝5，BC＝6时，连接BE，若∠ABE＝90°，求AE的长．